Hogyan segítsünk a szöveges feladatokkal küszködő diákoknak

“Ismerik a matematikát. Csak a szöveges feladatokat nem tudják megoldani. Az olvasásértésükkel van a baj.”

Hartwell asszony azt magyarázta, hogy a diákjai miért küszködtek az állami teszteken. Ismerte a diákjait, és bőséges felmérést végzett. Biztos volt benne, hogy a nehézségeik a szövegértéssel kapcsolatosak.

“Nem értem, miért teszik olyan nehézzé az olvasást. A gyerekek már így is nyelvi tesztet írnak.”

Egy New York-i program keretében kerültem össze Hartwell kisasszonnyal (és másokkal az iskolájában), amelynek célja a matematikai teljesítmény növelése volt. A cél az volt, hogy a koncepcionális matematikát bevigyék az “Tier 1” iskolákba. Az 1-es szintű iskolák azok voltak, amelyek három területen élen jártak a városban. A legalacsonyabb jövedelem, a legalacsonyabb teszteredmények és a színesbőrű tanulók legmagasabb aránya.

A programban részt vevő más tanároktól hallottam a “műveltségi” magyarázatot. És tényleg volt értelme. Ha a diákok tudták a matematikát, mi másért küszködtek volna a teszten, amely sok szöveges feladatot tartalmazott?

De volt egy bökkenő. Az elmúlt három évben az írni-olvasni tudás szintje városszerte 30-40% közé emelkedett. Ugyanebben az időszakban a matematikai eredmények többnyire változatlanok maradtak.

Ha ez egy olvasási probléma lenne, akkor az olvasási eredmények növekedésének robbanásszerű növekedést kellene eredményeznie a matematikában. Emellett a szöveges feladatok nyelvezete nem tűnt elég bonyolultnak ahhoz, hogy gondot okozzon.

A következő órán meg kellett látogatnom Ms. Hartwell osztályát. Szóproblémákkal kapcsolatos órát tervezett, így első kézből láthattam a problémát.

A szóproblémák túlszabályozása

A diákok kerek asztaloknál ültek, ő pedig elöl állt. Nála és a diákjainál mindannyiuknál kézi tábla volt.

Kinyitották a tankönyveiket a 47. oldalra, és ő hangosan felolvasott egy szófeladatot. “Sarah-nak 40 font répája van a lovai számára. Ha 100 lova van, hány fontot kap minden egyes ló?”

“Oké, osztály, van 40 fontja, amit minden lónak ad. Tehát milyen műveletre van szükségünk?”

Mutatott egy horgonytáblára, amelyen az egyes műveletek “kulcsszavai” voltak felsorolva. A ‘Mindegyik’ állt az osztálynévsor elején.

“Osztály!” – válaszolta az osztály.

“Rendben. Szóval hogyan osztunk el egy kis számot egy nagy számmal?”

Az osztály csendben volt. Ms Hartwell egy vinculumot (hosszú osztóházat) rajzolt a táblájára. A tanulók lemásolták, ahogy a 40-et a ház alá, a 100-at pedig kívülre tette.”

“Most a 100 nem fér bele a 40-be, ezért hozzá kell adnunk egy tizedest”. A 40-et 40,0-ra változtatta. “Hányszor fér bele a 100 a 400-ba?”

Néhány diák azt kiáltotta, hogy “Négy!”.

“Pontosan. Most már egy tizedesjegyet is be kell tennünk a hányadosunkba. A végső válaszunk?”

Az osztály leolvasta a tábláról a választ: “0,4”.

Kiosztott egy hasonló feladatot, és a falon lévő “CUBES” plakátra mutatott. “Ne feledjétek, hogy karikázzátok be a számokat, és jelöljétek be a kulcsszavakat.”

A tanulók munkája közben körbejárt. Néhányan megkérdezték, hova kell tenni a tizedesjegyet. Másoknak gondot okozott a hosszú osztás kivonási részének felsorakoztatása. Néhány diák párban dolgozott, az egyikük a számítást végezte, míg a másik lemásolta.

Az óra végére mindenkinek a papírján szerepelt a helyes válasz. “Látod?” Hartwell kisasszony megjegyezte: “Mindannyian tudják a matematikát.”

Mi ment rosszul?

Míg ez egy szélsőséges példa, Hartwell kisasszony sok hibája valójában elég gyakori.

Túlszabályozásról akkor beszélünk, amikor túl sok támogatást nyújtunk a tanulóknak. Míg a pedagógusok általában büszkék arra, hogy a tanulóknak “annyi támogatást nyújtanak, amennyire szükségük van”, a túlszabályozás más.

A “scaffolding” kifejezés Lev Vygotsky munkásságából származik. Ő alkotta meg a “proximális fejlődés zónája” kifejezést. A ZPD olyan dolgokat foglal magában, amelyek éppen csak elérhetetlenek a tanuló számára. Egyedül még nem tudják megcsinálni, de támogatással már igen. Az “állványozással” ezeket a készségeket át tudjuk helyezni a tanuló alapvető készségei közé.”

Az, amit gyakran figyelmen kívül hagynak, hogy az állványozás csak a tanuló ZPD-jében már meglévő készségekre vonatkozik. Egy egész sor olyan készség van, amely jelenleg a tanuló számára elérhetetlen. Amikor megpróbáljuk ezeket a készségeket állványozni, többet ártunk, mint használunk.

A túlzott állványozás egyik problémája, hogy a tanulók soha nem internalizálják a megcélzott készségeket. Ha egy tanulónak a ZPD-jén kívül eső dolgokban segítünk, mindig szüksége lesz a segítségünkre. Legalábbis addig, amíg nem azonosítjuk azokat a köztes készségeket, amelyek a ZPD-jükben vannak.

A másik probléma az, hogy a túlszabályozás a siker hamis érzetét kelti bennünk. Ebben az esetben Ms. Hartwell azt hitte, hogy a diákjai “meg tudják csinálni a matematikát” a szófeladatban. A valóságban azonban csak utánozták az ő cselekedeteit. Nem volt okuk azt hinni, hogy egyedül is képesek lennének hasonló megoldást találni.

A problémamegoldás folyamatából a “megfogalmazás” teljes folyamatát is kivette. Sok pedagógus a megértést és a megfogalmazást egy és ugyanazon dolognak tekinti, pedig a megfogalmazás külön matematikai kompetencia.

És lehet, hogy éppen ez az a hiányzó összetevő, ami hiányzik abból, ahogyan jelenleg a szóproblémákat tanítod.

Tantermi források és szakmai tanulás

Formulation: The Key to Success with Word Problems

A szóproblémák megfogalmazása magában foglalja azok megértését. De ezen túlmutat. A megfogalmazás inkább fordítás, mint megértés.

Amikor egy tanuló elolvas egy szóproblémát, először a betűket hangokká kell alakítania (dekódolás). Ezután meg kell értenie, hogy mit jelentenek a szavak (szókincs). Meg kell érteniük, hogyan illeszkednek a szavak egy mondatba (szintaktika). Végül a szövegértés abból adódik, hogy ezeket a részeket összerakják, hogy értelmet adjanak.

A legtöbb 6. osztályos tanuló el tudja olvasni Ms. Hartwell feladatát, és könnyen megérti, hogy Sarah répát osztogat a lovaknak. De sokkal kevesebben fogják összekapcsolni a répák “szétosztását” az osztással.

Ez az a rész, ami sok pedagógust zavarba hoz. Nekünk annyira nyilvánvalónak tűnik. “Szó szerint szétosztja a répákat. Hogyhogy nem látják, hogy ez osztás.”

Egyszerűen nem látják. Ha látnák, nem látnánk kulcsszavas táblákat lógni a matekórákon. És az egész visszanyúlik oda, amikor először tanítjuk a műveleteket.

Miért küzdenek a diákok a fogalmazással

Sok tanár sok iskolában azt tanítja a diákoknak, hogy a matematika az értelemalkotás tárgya. Másokban azonban a matematikát az emlékezés tantárgyaként tanítják.

A “matematika mint emlékezés” egyik példája az, amikor a diákok bemagolják a matematikai tényeket. De az algoritmusok is az emlékezésről szólnak. Tegyük a 120-at a 47-re. Kövesd ezeket a lépéseket az összeadáshoz, ezeket a kivonáshoz a kivonáshoz, és ezeket a szorzáshoz.

A tanulók anélkül ismételgethetik ezeket a lépéseket, hogy megértenék a számok méretét vagy akár azt is, hogy mit jelentenek a műveletek.

Ha fogalmakkal kezdjük (vizuális modellek vagy számmondatok segítségével), a tanulók megtanulják, mit jelentenek a műveletek. Amikor egyenesen egy algoritmusra térünk át, a tanulók a műveletekre úgy gondolnak, mint véletlenszerű lépések sorozatára.

A tanulóknak évről évre emlékezniük és ismételniük kell. Házi feladatra 30-szor végzik el ugyanazt az algoritmust. Változtassuk meg a számokat, és a folyamat ugyanaz marad. De adjunk nekik egy szófeladatot, és most már értelmet kell adniuk.”

Mit mondanak a tesztek a gondolkodásról

A könnyebbség kedvéért adhatnánk a diákjainknak 10 feladatot “Osztás szófeladat” címmel. Még csak el sem kell olvasniuk a feladatokat. Csak ki kell találniuk (vagy kitalálniuk), hogy melyik szám az osztó és melyik az osztott.

De amikor a diákok állami tesztet írnak, nem az a cél, hogy könnyebbé tegyük. A cél annak felmérése, hogy mire képesek önállóan.

A tesztkészítők nem akarják megmondani nekik, hogy milyen műveletet használjanak. Még az osztás és az összeadás kulcsszavait is beleteszik ugyanabba a feladatba. “Az osztályban 20 diák van. Ha minden gyereknek van három dollárja, akkor mennyi van összesen?”

Amikor tehát a diákok a szófeladatokkal küzdenek, nem csak a szófeladatokról van szó. Ez általában azt jelenti, hogy emlékezetből matekoznak. Meg kell tanítanunk nekik, hogy a matematika az értelemalkotásról szól.

A tanulóknak stratégiákra és folyamatra van szükségük a szöveges feladatok megoldásához

A probléma egy olyan rendszerrel, mint a CUBES, részben az, hogy stratégiának nevezi magát, de valójában egy folyamat.

A folyamat lépések sorozata. Ha egyszer azonosítottál egy hatékony folyamatot, akkor azt újra és újra megismételheted anélkül, hogy túl sokat gondolkodnál rajta. Az algoritmusok is egy folyamat. Ahogy a “legmagasabbtól a legrövidebbig” való felsorakozás is az ebédhez vezető sétához.

A stratégia más. A stratégiák mély megértést igényelnek. És a megértés új helyzetekben való alkalmazásának képességét.

Nem készíthetjük fel a tanulókat minden olyan forgatókönyvre, amellyel egy szöveges feladatban találkozhatnak. Egyesek megkövetelik, hogy különböző matematikai készségeket kombináljanak, amelyeket korábban még soha nem kombináltak. Vagy megkövetelhetik, hogy a tanulók megváltoztassák a lépések sorrendjét, hogy eljussanak a helyes megoldáshoz.

Gondoljunk a következőkre:

Egy iskolai rendezvényre, amelyen 100 diák vesz részt, 5 gallon gyümölcslé áll rendelkezésedre. Ha minden pohárba 3 uncia fér, hány poharat ihat minden diák? Mennyi marad belőle.”

Egy problémamegoldó folyamat segíthet a tanulóknak abban, hogy elkezdjék megoldani ezt a problémát. “Határozd meg, hogy mit kérdeznek”. “Fontolja meg, milyen információt adnak meg.”

De nincs olyan meghatározott folyamat, amelyet megtaníthatnánk nekik a tényleges megoldásra. Itt jön a képbe a stratégia. Át kell számolniuk az egységeket. Fel kell ismerniük, hogy maradékkal osztunk, nem pedig teljesen osztunk. Valószínűleg át kellene rendezniük a műveleteket is, a gyümölcslé poharakra való felosztása előtt a tanulók számával való osztás előtt.

Nincs olyan “trükk”, amivel a tanulók eljutnának odáig. Meg kell érteniük a műveletek jelentését. Meg kell érteniük a matematikát, mint értelmet adó tárgyat. És ismételten gyakorolniuk kell a stratégiai gondolkodás alkalmazását a szófeladatokra.

A Polya-folyamat a szófeladatok megoldására

Pólya György befolyásos magyar matematikus és stanfordi professzor volt, aki talált egy eljárást, amely bármilyen probléma megoldására alkalmazható. Munkássága számtalan matematikust és pedagógust érintett meg, akik közül a legtöbben nem ismerik a nevét.

Sőt, a CUBES és más úgynevezett problémamegoldó stratégiák lazán az ő munkáján alapulnak. A probléma az, hogy megpróbálják leegyszerűsíteni. Eközben eltávolítanak mindent, ami az elmélyült gondolkodásra hasonlít.

Polya úgy vélte, hogy minden probléma négy lépésben megoldható: Megértés, tervezés, megoldás és reflexió. Szerintem Polya eredeti négylépcsős folyamata éppen megfelel az iskolai használatra.

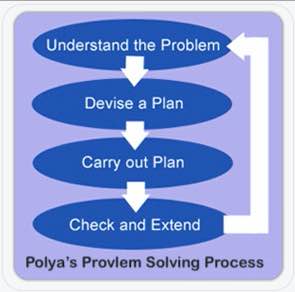A probléma megértéséhez azonosítjuk, milyen információk adottak, és mit akarunk megtalálni. Innen származik a “C” és az “U” a kockákban. Ha a diákok be akarják karikázni a számokat és aláhúzni a kérdést, rendben. Én jobban szeretem, ha leírják őket (egységekkel együtt) egy grafikus szervezőbe, legalábbis kezdetben. Ez segít nekik feldolgozni az olvasottakat. Nekem, mint tanárnak is segít felmérni a megértésüket, miközben körbejárom a termet.

A következő a trükkös rész. A “terv” az, ahol megfogalmazzuk a problémát. Fogunk egy valós világbeli forgatókönyvet, és egy másik matematikai ábrázolássá alakítjuk.

A harmadik lépés a megoldás. Ha helyesen fogalmaztunk, akkor ez az a pont, ahol számolunk. A tanulók általában algoritmust használnak, de bátorítom az egyenletek és a vizuális modellek használatát is.

Végül a tanulók visszanéznek és ellenőrzik a munkájukat. A folyamatukra is reflektálniuk kell. Ha hibáztam, miért? Segíthet-e ez a stratégia a jövőben hasonló problémák megoldásában?

Szöveges feladatok megoldásának stratégiái

Az, hogy van egy folyamat a szöveges feladatok megközelítéséhez, mindenképpen hasznos. De nem tehetünk úgy, mintha az értelmes matematikát csak a lépések követésével tanulnánk meg. A szóproblémák lényege, hogy a matematikát a “matematikai tényeken” és az algoritmusokon túlra is kiterjesszük.

Létezik néhány hasznos stratégia, amely segít a tanulóknak a megfogalmazásban. Eleinte kifejezetten többféle stratégiát tanítok.

Amint megtanítom a stratégiákat, a diákokkal olyan feladatokat oldatok meg, amelyek jól illeszkednek az adott stratégiához. Egyes problématípusokhoz nagyon jól illik a “Találd ki és ellenőrizd”. Másokhoz jobban illik a “Rajzolj egy képet”.

Végül olyan kihívást jelentő szöveges feladatokat adok nekik, amelyeket többféleképpen is meg lehet oldani. Ha már megvan az eszközkészletük, kiválaszthatják, melyik a legjobb az adott helyzetben.

A stratégiák kombinálása is nagyon hatékony lehet. Például egy kép lerajzolása gyakran segíthet a megfogalmazásban. Ha egy gazdának 18 sor sárgarépája van, és minden sorban 10 sárgarépa van, a tanuló kezdheti azzal, hogy lerajzolja a mezőt. Egy bizonyos ponton azt gondolhatják, hogy “Hű, ez egy tömb”, és rájönnek, hogy a szorzást mentális matematika, egy kifejezés vagy egy algoritmus segítségével végezhetik el.”

Máskor a tanulók vizuális modelleket használhatnak a probléma megfogalmazásához és megoldásához.

Segítse diákjait a kihívást jelentő szóproblémák kezelésében

Ha sok tanárhoz hasonlóan ön is aggódhat, hogyan fogják mindezt kezelni a diákjai. Folyamatok, stratégiák, kritikus gondolkodás… sok mindenről van szó.

Még arra is gondolhatsz, hogy a szóproblémák e cikk előtt könnyebbnek tűntek. Ha így van, akkor elnézést kérek.

A kulcs az, hogy ne essünk túlterheltek, ha egyszerre akarunk mindent megcsinálni. Kezdje egy egyszerű szóprobléma megoldásával Polya eljárásának segítségével. Ezután minden héten vezess be egy új stratégiát. Az év végére meg fogsz lepődni, milyen messzire jutottak.

Még mélyebbre akarsz menni a kreatív problémamegoldásban. Fontolja meg, hogy részt vegyen egy gyakorlati matematikai workshopon, vagy dolgozzon együtt egy online trénerrel.

Ha készen áll arra, hogy holnap egy kis Polyát vigyen az osztályterembe, ez a grafikus szervező remek kiindulópont. Segítséget nyújt a négylépcsős folyamathoz, és segít azonosítani, hogy a diákok hol térnek el a helyes útról.

Free Word Problem Organizer

A szerzőről

Jeff Lisciandrello a Room to Discover alapítója és a diákközpontú tanulásra szakosodott oktatási tanácsadó. Az általa kidolgozott 3-híd tervezése a tanuláshoz segít az iskoláknak innovatív gyakorlatok felfedezésében a hagyományos keretek között. Szívesen segít a pedagógusoknak a kutatásalapú és személyre szabott oktatási megközelítések alkalmazásában. A Twitteren @EdTechJeff

keresztül lehet vele kapcsolatba lépni.