Hogyan lehet nagy számokat gyorsan szorozni

Itt megtanuljuk az oszd meg és uralkodj algoritmus zseniális alkalmazását lineáris algebrával kombinálva nagy számok gyors szorzására. És bevezetés a big-O jelölésbe!

Ez az eredmény valójában annyira ellentmond az intuíciónak, hogy a nagy matematikus Kolmogorov azt feltételezte, hogy ilyen gyors algoritmus nem létezik.

0. rész: A hosszú szorzás lassú szorzás. (És bevezetés a Big-O jelölésbe)

Mindannyian emlékszünk arra, hogy az iskolában tanultunk szorozni. Sőt, be kell vallanom valamit. Ne feledjétek, ez egy ítélkezésmentes zóna 😉

Az iskolában “vizes játék” volt, amikor túlságosan esett az eső ahhoz, hogy a játszótéren játsszunk. Míg a többi (normális/szórakozni szerető/pozitív jelzőt választó) gyerek játszott és hülyéskedett, én néha fogtam egy papírlapot és összeszoroztam nagy számokat, csak úgy a kedvemért. A számolás puszta öröme! Még szorzási versenyünk is volt, a “Szuper 144″, ahol egy 12-szer 12-es számokból (1-től 12-ig) álló, összekevert rácsot kellett a lehető leggyorsabban összeszoroznunk. Ezt vallásos módon gyakoroltam, olyannyira, hogy saját, előre elkészített gyakorló lapjaim voltak, amelyeket lefénymásoltam, és váltakozva használtam. Végül 2 perc 1 másodpercre csökkentettem az időmet, aminél a firkálás fizikai határát elértem.”

A szorzás eme megszállottsága ellenére soha nem jutott eszembe, hogy ezt jobban is meg lehetne csinálni. Nagyon sok órát töltöttem szorzással, de soha nem próbáltam javítani az algoritmuson.

Gondoljunk csak a 103 szorzására 222-vel.

Kiszámoljuk 2szer 3szor 1 +2szer 0szor 10 + 2szor 1szer 100 + 20szor 3szor 1 + 20szor 0szor 10 + 20szor 1szer 100 = 22800

Az n jegyű számok szorzásához általában O(n²) művelet szükséges. A “nagy-O” jelölés azt jelenti, hogy ha a műveletek számát az n függvényében ábrázolnánk, akkor valójában az n² kifejezés számít. Az alakja lényegében kvadratikus.

Ma teljesítjük gyermekkori álmainkat, és továbbfejlesztjük ezt az algoritmust. De előbb! Big-O vár ránk.

Big-O

Nézzük meg az alábbi két gráfot

Kérdezz meg egy matematikust, hogy “x² és x²+x^(1/3) ugyanaz?”, és valószínűleg belehánynak a kávéscsészéjükbe, sírni kezdenek, és motyognak valamit a topológiáról. Legalábbis én (először) így reagáltam, pedig alig tudok valamit a topológiáról.

Oké. Ezek nem ugyanazok. De a mi számítógépünket nem érdekli a topológia. A számítógépek teljesítménye annyi mindenben különbözik, amit nem is tudok leírni, mert semmit sem tudok a számítógépekről.

De egy gőzhenger finomhangolásának semmi értelme. Ha két függvény a bemenetük nagy értékei esetén ugyanolyan nagyságrendben növekszik, akkor gyakorlati szempontból ez tartalmazza a legtöbb releváns információt.

A fenti grafikonon azt látjuk, hogy a két függvény nagy bemenetek esetén eléggé hasonlóan néz ki. De ugyanígy az x² és a 2x² is hasonló – az utóbbi csak kétszer akkora, mint az előbbi. Az x = 100-nál az egyik 10 000, a másik pedig 20 000. Ez azt jelenti, hogy ha az egyiket ki tudjuk számítani, akkor valószínűleg a másikat is ki tudjuk számítani. Míg egy exponenciálisan növekvő függvény, mondjuk 10^x, x = 100-nál már jóval nagyobb, mint az atomok száma a világegyetemben. (10¹⁰⁰ >>>>> 10⁸⁰, ami egy becslés, az Eddington-szám, az univerzumban lévő atomok számára a guglizásom* szerint).

*Tényleg a DuckDuckGo-t használtam.

Egész számokat polinomként írni egyszerre nagyon természetes és nagyon természetellenes. Az 1342 = 1000 + 300 + 40 + 2 írása nagyon természetes. Az 1342 = x³+3x²+4x + 2 írása, ahol x = 10, kissé furcsa.

Általában tegyük fel, hogy két nagy számot akarunk szorozni, b bázisban írva, egyenként n számjeggyel. Mindkét n számjegyű számot polinomként írjuk fel. Ha az n számjegyű számot r darabra osztjuk, akkor ez a polinom n/r tagból áll.

Legyen például b = 10, r = 3, és a számunk 142,122,912

Ezt átalakíthatjuk

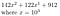
Ez nagyon szépen működik, ha r = 3, és a 10-es bázison írt számunknak 9 számjegye volt. Ha r nem osztja tökéletesen az n-t, akkor egyszerűen hozzáadhatunk néhány nullát az elejére. Ezt megint egy példával lehet a legjobban szemléltetni:

27134 = 27134 + 0*10⁵ = 027134, amit úgy ábrázolunk, hogy

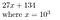
Miért lehet ez hasznos? A P polinom együtthatóinak megtalálásához, ha a polinom N rendű, akkor N+1 ponton történő mintavételezéssel meghatározhatjuk az együtthatóit.

Ha például az x⁵ + 3x³ +4x-2 polinomot, amely 5 rendű, 6 pontban mintavételezzük, akkor ki tudjuk számolni a teljes polinomot.

Intuitív módon egy 5 rendű polinomnak 6 együtthatója van: 1, x, x, x², x³, x⁴, x⁵ együtthatója. Adva 6 értéket és 6 ismeretlent, meg tudjuk állapítani az értékeket.

(Ha ismered a lineáris algebrát, akkor az x különböző hatványait lineárisan független vektorokként kezelheted, készíthetsz egy mátrixot az információ ábrázolására, invertálhatod a mátrixot, és voilá)

Polinomok mintavétele az együtthatók meghatározásához (választható)

Itt egy kicsit mélyebben megvizsgáljuk a polinom mintavételezésének logikáját az együtthatók levezetéséhez. Nyugodtan ugorjunk a következő szakaszra.

Azt fogjuk megmutatni, hogy ha két N fokú polinom N+1 ponton megegyezik, akkor azonosnak kell lenniük. Vagyis N+1 pont egyértelműen meghatározza az N rendű polinomot.

Nézzünk egy 2-es rendű polinomot. Ez az alakja P(z) = az² +bz + c. Az algebra alaptétele alapján – szégyentelenül, dugó ide, több hónapot töltöttem azzal, hogy összeraktam ennek a bizonyítását, majd megírtam, itt – ez a polinom faktorizálható. Ez azt jelenti, hogy felírhatjuk A(z-r)(z-w)

Megjegyezzük, hogy z = r-nél és z = w-nél a polinom értéke 0. Azt mondjuk, hogy w és r a polinom gyökei.

Most megmutatjuk, hogy P(z)-nek nem lehet kettőnél több gyöke. Tegyük fel, hogy három gyöke van, ezeket nevezzük w, r, s. Ezután faktorizáljuk a polinomot. P(z) = A(z-r)(z-w). Akkor P(s) = A(s-r)(s-w). Ez nem egyenlő 0-val, mivel a nem nulla számok szorzása nem nulla számot ad. Ez ellentmondás, mert az eredeti feltételezésünk az volt, hogy s a P polinom gyöke.

Ez az érvelés lényegében azonos módon alkalmazható egy N rendű polinomra.

Tegyük fel, hogy két N rendű P és Q polinom N+1 pontban megegyezik. Akkor, ha különböznek, akkor P-Q olyan N-rendű polinom, amely N+1 pontban 0. Az előzőek szerint ez lehetetlen, mivel egy N rendű polinomnak legfeljebb N gyöke van. Tehát a feltételezésünk téves lehetett, és ha P és Q N+1 pontban megegyezik, akkor ugyanaz a polinom.

A látás hit: Egy kidolgozott példa

Nézzünk egy igazán nagy számot, amelyet p-nek nevezünk. 10-es bázisban p 24 számjegy hosszú (n=24), és 4 darabra osztjuk (r=4). n/r = 24/4 = 6

p = 292,103,243,859,143,157,364,152.

Az ezt reprezentáló polinomot pedig nevezzük P-nek,

P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152

mivel P(10⁶) = p.

Mivel ennek a polinomnak a foka 3, az összes együtthatót ki tudjuk számolni 4 helyen történő mintavételből. Nézzük meg, mi történik, ha néhány helyen mintavételezünk.

• P(0) = 364,152
• P(1) = 1,043,271
• P(-1) = 172,751
• P(2) = 3,962,726

Feltűnő, hogy ezek mind 6 vagy 7 számjegyűek. Ehhez képest a p-ben eredetileg 24 számjegy található.

Szorozzuk be p-t q-val. Legyen q = 124,153,913,241,143,634,899,130, és

Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130

A t=pq kiszámítása szörnyű lehet. De ahelyett, hogy ezt közvetlenül tennénk, megpróbáljuk kiszámítani t polinomiális reprezentációját, amit T-vel jelölünk. Mivel P egy r-1=3 rendű polinom, Q pedig egy r-1=3 rendű polinom, T egy 2r-2=6 rendű polinom.

T(10⁶) = t = pq

T(10⁶) = P(10⁶)Q(10⁶)

A trükk az, hogy a T együtthatóit fogjuk kiszámítani, nem pedig közvetlenül összeszorozzuk p és q együtthatóit. Ezután a T(1⁰⁶) kiszámítása egyszerű, mert az 1⁰⁶-val való szorzáshoz csak 6 nullát ragasztunk hátra. Az összes rész összegzése is könnyű, mert az összeadás egy nagyon alacsony költségű művelet a számítógépek számára.

A T együtthatóinak kiszámításához 2r-1 = 7 ponton kell mintavételeznünk, mert ez egy 6 rendű polinom. Valószínűleg kis egész számokat akarunk választani, ezért

• T(0)=P(0)Q(0)= 364,152*899,130
• T(1)=P(1)Q(1)= 1,043,271*2,080,158
• T(2)=P(2)Q(2)= 3,962,726*5,832,586
• T(-1)=P(-1)Q(-1)= 172751*1544584
• T(-2)=P(-2)Q(-2)= -1,283,550*3,271,602
• T(3)=P(-3)Q(-3)= -5,757,369*5,335,266

Megjegyezzük a P(-3), Q(-3), P(2), Q(2) stb. méretét…. Ezek mind olyan számok, amelyek megközelítőleg n/r = 24/4 = 6 számjegyűek. Némelyik 6 számjegyű, némelyik 7 számjegyű. Ahogy n egyre nagyobb lesz, ez a közelítés egyre ésszerűbbé válik.

Ezidáig a problémát a következő lépésekre, illetve algoritmusra redukáltuk:

(1) Először kiszámítjuk P(0), Q(0), P(1), Q(1), stb (alacsony költségű művelet)

(2) Hogy megkapjuk T(x) 2r-1= 7 értékét, most 2r-1 n/r számjegyű közelítő méretű számot kell megszoroznunk. Nevezetesen ki kell számolnunk P(0)Q(0), P(1)Q(1), P(-1)Q(-1), stb. (Nagy költségű művelet)

(3) Rekonstruáljuk a T(x) értéket az adatpontjainkból. (Alacsony költségű művelet: de majd később kerül szóba).

(4) A rekonstruált T(x)-ünkkel értékeljük ki T(10⁶) ebben az esetben

Ez szépen elvezet a megközelítés futási idejének elemzéséhez.

Futási idő

A fentiekből kiderült, hogy az (1) és (3) alacsony költségű műveleteket ideiglenesen figyelmen kívül hagyva, két n számjegyű szám Toom algoritmusával történő szorzásának költségei a következőknek engedelmeskednek:

Ezt láttuk a kidolgozott példában. Minden P(0)Q(0), P(1)Q(1) stb. szorzása T(n/r)-be kerül, mert két körülbelül n/r hosszúságú számot szorzunk. Ezt 2r-1-szer kell megtennünk, mivel T(x) – lévén 2r-2 rendű polinom – 2r-1 helyen akarunk mintát venni.

Milyen gyors ez? Egy ilyen egyenletet explicit módon is meg tudunk oldani.

Most már csak néhány kusza algebra

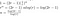
Mert a mátrixszorzás (“újra összerakás”) folyamatának volt még néhány költsége, és az összeadásból, nem igazán mondhatjuk, hogy a megoldásunk a pontos futási idő, így ehelyett arra következtetünk, hogy megtaláltuk a futási idő nagy-O-ját

Optimalizálás r

Ez a futási idő még mindig r-től függ. Javítsuk ki az r-t, és kész is vagyunk. De kíváncsiságunkat még nem elégítettük ki!

Amint n egyre nagyobb lesz, szeretnénk egy megközelítőleg optimális értéket találni az r megválasztásához. Vagyis olyan r értéket akarunk választani, amely n különböző értékeire változik.

A legfontosabb dolog itt az, hogy r változása esetén némi figyelmet kell fordítanunk az újra összerakási költségre – az ezt a műveletet végrehajtó mátrix költsége O(r²). Amikor r fix volt, erre nem kellett figyelnünk, mert ahogy n nagyra nőtt r fixálása mellett, az n-t tartalmazó kifejezések voltak azok, amelyek meghatározták a növekedést, hogy mennyi számítás szükséges. Mivel az r optimális választása az n növekedésével egyre nagyobb lesz, ezt már nem hagyhatjuk figyelmen kívül.

Ez a különbségtétel döntő fontosságú. Elemzésünk kezdetben r egy értékét választotta, talán 3-at, talán 3 milliárdot, majd a big-O méretét nézte, ahogy n tetszőlegesen nagyra nőtt. Most megnézzük a viselkedést, ahogy n tetszőlegesen nagyra nő, és r az n-nel együtt nő valamilyen általunk meghatározott ütemben. Ez a szemléletváltás az O(r²)-t változónak tekinti, míg amikor r-t fixen tartottuk, az O(r²) egy konstans volt, bár nem ismertük.

Az előző elemzésünket tehát frissítjük:

ahol az O(r²) az újra összerakási mátrix költségét jelenti. Most az n minden értékéhez olyan r értéket akarunk választani, amely megközelítőleg minimalizálja ezt a kifejezést. A minimalizáláshoz először megpróbáljuk differenciálni r tekintetében. Ez a kissé förtelmesnek tűnő kifejezést

Normális esetben a minimumpont megtalálásához a deriváltat 0-val egyenlővé tesszük. De ennek a kifejezésnek nincs szép minimuma. Ehelyett egy “elég jó” megoldást keresünk. Vendégértékként r = r^(sqrt(logN)) értéket használunk. Grafikusan ez elég közel van a minimumhoz. (Az alábbi ábrán az 1/1000 faktor azért van, hogy a grafikon ésszerű méretarányban is látható legyen)

A lenti grafikonon a T(N) függvényünk egy konstanssal skálázva, piros színnel látható. A zöld vonal az x = 2^sqrt(logN) értéknél van, ami a vendégértékünk volt. Az “x” az “r” helyét veszi át, és mindhárom képen N különböző értékét használjuk.

Ez eléggé meggyőző számomra, hogy jól döntöttünk. Az r-nek ezt a választását bedughatjuk, és láthatjuk, hogy az algoritmusunk végső nagy-O:

ahol egyszerűen bedugtuk az r értékét, és a log(2r-1)/log(r) közelítést használtuk, ami nagyon pontos r nagy értékeinél.

Mekkora a javulás?

Talán ésszerű volt, hogy nem vettem észre ezt az algoritmust, amikor kisfiúként szorzást végeztem. Az alábbi grafikonon a big-O függvényünk együtthatóját 10-nek adom (a szemléltetés kedvéért), és elosztom x²-vel (mivel a szorzás eredeti megközelítése O(n²) volt. Ha a piros vonal 0 felé tendál, az azt mutatná, hogy az új futási időnk aszimptotikusan jobban teljesít, mint O(n²).

És valóban, bár a függvény alakja azt mutatja, hogy a mi megközelítésünk végül gyorsabb, és végül sokkal gyorsabb, ahhoz, hogy ez így legyen, meg kell várnunk, amíg közel 400 számjegyű hosszú számokat kapunk! Még ha az együttható csak 5 is lenne, a számoknak körülbelül 50 számjegyűnek kellene lenniük ahhoz, hogy sebességnövekedést tapasztaljunk.

A 10 éves énem számára a 400 számjegyű számok szorzása egy kicsit nehéz lenne! A függvényem különböző rekurzív hívásainak nyomon követése is kissé ijesztő lenne. De egy számítógép számára, amely a mesterséges intelligencia vagy a fizika területén végez feladatot, ez gyakori probléma!

Milyen mélyreható ez az eredmény?

Azt szeretem ebben a technikában, hogy nem rakétatudomány. Nem a legelképesztőbb matematika, amit valaha is felfedeztek. Utólag talán nyilvánvalónak tűnik!

Mégis ez a matematika zsenialitása és szépsége. Olvastam, hogy Kolmogorov egy szemináriumon feltételezte, hogy a szorzás alapvetően O(n²). Kolmogorov alapvetően sok modern valószínűségelméletet és analízist talált fel. A 20. század egyik legnagyobb matematikusa volt. Mégis, amikor erről a nem kapcsolódó területről volt szó, kiderült, hogy egy egész tudástömeg vár felfedezésre, amely az ő és mindenki más orra előtt hevert!

Valójában az oszd meg és uralkodj algoritmusok ma elég gyorsan eszünkbe jutnak, mivel olyan gyakran használják őket. De ezek a számítógépes forradalom termékei, amennyiben csak a hatalmas számítási teljesítménynek köszönhetően az emberi elmék kifejezetten a számítási sebességre, mint a matematika önállóan tanulmányozásra érdemes területére koncentráltak.

Ez az oka annak, hogy a matematikusok nem hajlandóak csak azért elfogadni, hogy a Riemann-hipotézis igaz, mert úgy tűnik, hogy igaz lehet, vagy hogy P nem egyenlő NP-vel, csak mert ez tűnik a legvalószínűbbnek. A matematika csodálatos világa mindig megőrzi azt a képességét, hogy megzavarja a várakozásainkat.

Sőt, még gyorsabb módot is találhatunk a szorzásra. A jelenlegi legjobb megközelítések gyors Fourier-transzformációkat használnak. De ezt egy másik napra tartogatom 🙂

Mondd el a gondolataidat lentebb. Újabban a Twitteren ethan_the_mathmo néven vagyok, itt tudsz követni.

Ezzel a problémával Moore és Mertens fizikusok “The Nature of Computation” című csodálatos könyvében találkoztam, ahol az egyik probléma végigvezet a Toom algoritmusának elemzésén.