Posted on 29th November 2018 by Maximilian Siebert
A heterogenitástól nem kell félni, csupán azt jelenti, hogy az adatokban variabilitás van. Tehát, ha valaki különböző tanulmányokat hoz össze elemzésükhöz vagy metaanalízis elvégzéséhez, egyértelmű, hogy különbségeket fog találni. A heterogenitás ellentéte a homogenitás, ami azt jelenti, hogy minden tanulmány ugyanazt a hatást mutatja.
Fontos megjegyezni, hogy a heterogenitásnak különböző típusai vannak:
- Klinikai: Különbségek a résztvevőkben, a beavatkozásokban vagy az eredményekben
- Módszertani: Különbségek a vizsgálati tervben, a torzítás kockázata
- Statisztikai: Változás a beavatkozás hatásaiban vagy eredményeiben
Ezek a különbségek azért érdekelnek minket, mert jelezhetik, hogy a beavatkozásunk nem minden alkalommal ugyanúgy működik. Ezen különbségek vizsgálatával sokkal jobban megérthetjük, hogy milyen tényezők befolyásolják a beavatkozást, és milyen eredményre számíthatunk a beavatkozás következő alkalmazásakor.
Noha a klinikai és módszertani heterogenitás fontos, ez a blog a statisztikai heterogenitásra fog összpontosítani.
Hogyan lehet azonosítani és mérni a heterogenitást
A szemgolyópróba
Az erdődiagramban inkább az átfedő konfidenciaintervallumokat nézze meg, mint azt, hogy a hatásbecslések melyik oldalon vannak. Az, hogy az eredmények a hatás nélküli vonal mindkét oldalán vannak-e, nem feltétlenül befolyásolja annak megítélését, hogy van-e heterogenitás, de befolyásolhatja annak megítélését, hogy a heterogenitás számít-e.
Ezt szem előtt tartva nézze meg az alábbi grafikont, és döntse el, melyik grafikon a homogénebb.
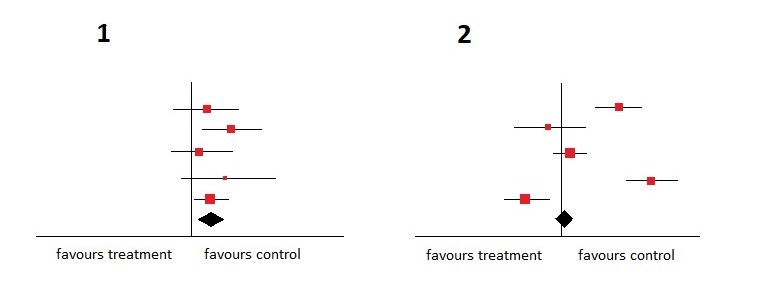
A homogénebb természetesen az 1-es számú grafikon . A konfidenciaintervallumok mind átfedik egymást, ráadásul minden tanulmány a kontroll beavatkozást részesíti előnyben.
Azoknak, akik szeretnek mérni a dolgokat ahelyett, hogy csak szemrevételeznék, ne aggódjanak, van még néhány statisztikai módszer, amely segít megragadni a heterogenitás fogalmát.
Chi-négyzet (χ²) teszt
Ez a teszt azt a nullhipotézist feltételezi, hogy az összes vizsgálat homogén, vagy hogy minden vizsgálat azonos hatást mér, és egy p-értéket ad nekünk e hipotézis tesztelésére. Ha a teszt p-értéke alacsony, akkor elvethetjük a hipotézist, és heterogenitás áll fenn.
Mivel a teszt gyakran nem elég érzékeny, és a heterogenitás téves kizárása gyorsan megtörténik, sok tudós < 0,05 helyett < 0,1 p-értéket használ határértékként.
I²
Ezt a tesztet Julian Higgins professzor fejlesztette ki, és elmélete szerint a heterogenitás mértékét méri, nem pedig azt állapítja meg, hogy jelen van-e vagy sem.
Az I² értelmezésének küszöbértékei félrevezetőek lehetnek, mivel az inkonzisztencia fontossága több tényezőtől függ. Az értelmezéshez egy durva útmutató a következő:
- 0%-40%: talán nem fontos
- 30%-60%: mérsékelt heterogenitás
- 50%-90%: jelentős heterogenitás
- 75%-100%: jelentős heterogenitás
A fenti elmélet megértéséhez nézzük meg a következő példát.
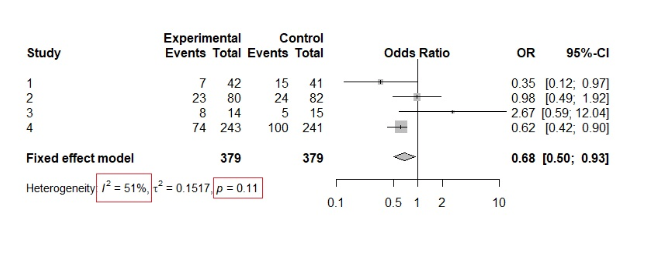
Láthatjuk, hogy a chi-négyzet teszt p-értéke 0,11, ami megerősíti a nullhipotézist, és így homogenitásra utal. A beavatkozásokat vizsgálva azonban már láthatunk némi heterogenitást az eredményekben. Továbbá az I²-érték 51%, ami mérsékelt vagy jelentős heterogenitásra utal.
Ez egy jó példa arra, hogy a χ²-teszt félrevezető lehet, ha csak néhány tanulmány szerepel a metaanalízisben.
Hogyan kezeljük a heterogenitást?
Ha már felfedeztük az eredményekben a változékonyságot, akkor kezelnünk kell azt. Íme néhány lépés, hogyan kezelheti ezt a problémát:
- Az adatokat ellenőrizze hibák szempontjából – Menjen vissza, és nézze meg, hogy esetleg valamit rosszul írt-e be
- Ne végezzen metaanalízist, ha a heterogenitás túl nagy – Nem minden szisztematikus áttekintéshez van szükség metaanalízisre
- Feltárja a heterogenitást – Ez történhet alcsoport-elemzéssel vagy metaanalízissel.regresszióval
- Végezzen véletlenszerű hatások meta-analízisét – Tartsa szem előtt, hogy ez a megközelítés olyan heterogenitásra vonatkozik, amelyet nem lehet megmagyarázni, mert az a véletlenből adódik
- Változtassa a hatásmértékeket – Tegyük fel, hogy a kockázati különbséget használja, és magas a heterogenitás, akkor próbálja ki a kockázati arányt vagy az esélyhányadost
(1) Fletcher, J. Mi a heterogenitás és fontos-e? BMJ 2007; 334 :94
(2) Deeks JJ, Higgins JPT, Altman DG (szerkesztők). 9. fejezet: Az adatok elemzése és metaanalízisek végzése. In: Higgins JPT, Green S (szerkesztők). Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 . The Cochrane Collaboration, 2011. Elérhető: www.cochrane-handbook.org.
(3) https://www.mathsisfun.com/data/chi-square-test.html
.