A gráfok különböző típusai léteznek a csúcsok számától, az élek számától, az összekapcsolhatóságtól és az általános szerkezetüktől függően. Ebben a fejezetben csak néhány fontos gráftípust fogunk tárgyalni.
Null gráf
Az élekkel nem rendelkező gráfot null gráfnak nevezzük.
Példa

A fenti gráfban három csúcs van, amelyek neve “a”, “b” és “c”, de nincs köztük él. Ezért ez egy null gráf.
Triviális gráf
Az olyan gráfot, amelynek csak egy csúcsa van, triviális gráfnak nevezzük.
Példa
A fent látható gráfban csak egy ‘a’ csúcs van, más élek nélkül. Ezért ez egy triviális gráf.
Nem irányított gráf
A nem irányított gráf tartalmaz éleket, de az élek nem irányítottak.
Példa
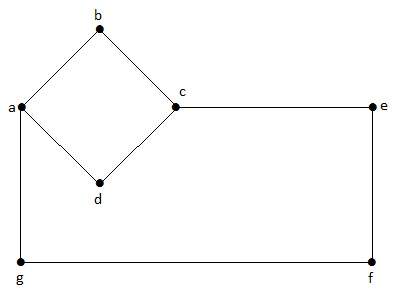
Ebben a gráfban ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ a csúcsok, és ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ a gráf élei. Mivel ez egy nem irányított gráf, az ‘ab’ és ‘ba’ élek azonosak. Hasonlóképpen a többi élt is ugyanígy tekintjük.
irányított gráf
Az irányított gráfban minden élnek van egy iránya.
Példa
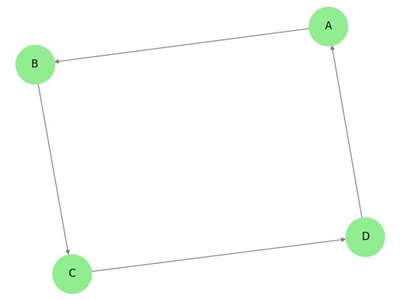
A fenti gráfban hét csúcsa van ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’ és ‘g’, és nyolc éle ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’ és ‘ga’. Mivel ez egy irányított gráf, minden élen egy nyíl jelzi az irányát. Megjegyezzük, hogy egy irányított gráfban az ‘ab’ különbözik a ‘ba’-tól.
Egyszerű gráf
Egy olyan gráfot, amelyben nincsenek hurkok és nincsenek párhuzamos élek, egyszerű gráfnak nevezzük.
-
Az ‘n’ csúcsú gráfban lehetséges élek maximális száma nC2, ahol nC2 = n(n – 1)/2 .
-
Az ‘n’ csúcsokkal lehetséges egyszerű gráfok száma = 2nc2 = 2n(n-1)/2.
Példa
A következő gráfban 3 csúcson 3 él van, ami a párhuzamos élek és hurkok nélkül a maximum. Ez a fenti képletek segítségével bizonyítható.
Az élek maximális száma n=3 csúccsal –
nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges
Az egyszerű gráfok maximális száma n=3 csúccsal –
2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8
Ez a 8 gráf az alábbiakban látható –
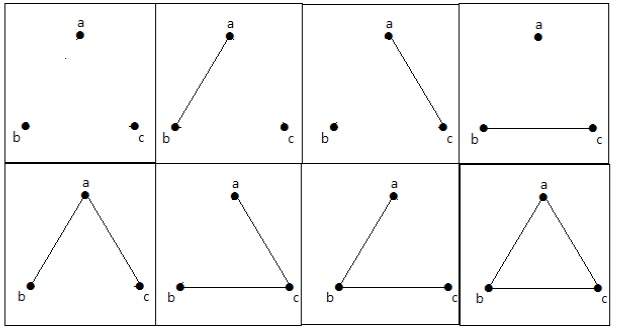
Kötött gráf
Egy G gráfot akkor mondjuk összefüggőnek, ha minden csúcspár között létezik egy út. A gráf minden csúcsához legalább egy élnek kell tartoznia. Így azt mondhatjuk, hogy az él másik oldalán lévő valamelyik másik csúcshoz kapcsolódik.
Példa
A következő gráfban minden csúcsnak van saját éle, amely más élekhez kapcsolódik. Ezért ez egy összefüggő gráf.
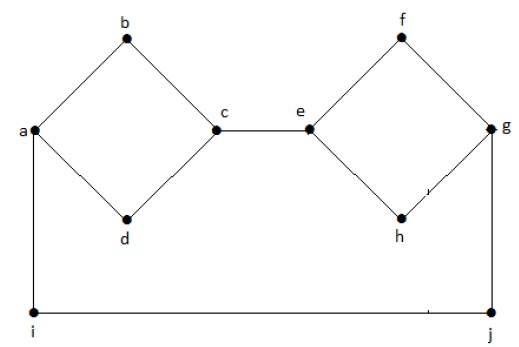
Összefüggő gráf
Egy G gráf akkor összefüggéstelen, ha nem tartalmaz legalább két összefüggő csúcsot.
1. példa
A következő gráf egy példa a Disconnected Graphra, ahol két komponens van, az egyiknek ‘a’, ‘b’, ‘c’, ‘d’ csúcsai vannak, a másiknak pedig ‘e’, ‘f’, ‘g’, ‘h’ csúcsai.
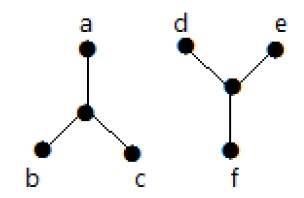
A két komponens független és nem kapcsolódik egymáshoz. Ezért nevezzük összefüggéstelen gráfnak.
2. példa
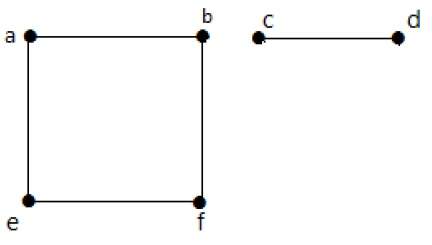
Ebben a példában két független komponens van, a-b-f-e és c-d, amelyek nem kapcsolódnak egymáshoz. Ezért ez egy összefüggéstelen gráf.
Reguláris gráf
Egy G gráfot szabályosnak mondunk, ha minden csúcsa azonos fokú. Ha egy gráfban minden egyes csúcs fokozata ‘k’, akkor a gráfot ‘k-szabályos gráfnak’ nevezzük.
Példa
A következő gráfokban minden csúcsnak ugyanaz a foka. Ezeket a gráfokat tehát szabályos gráfoknak nevezzük.
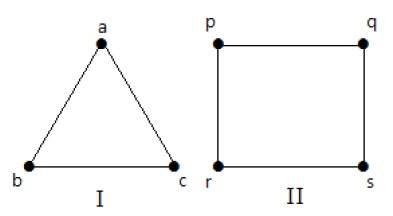
Mindkét gráfban minden csúcs 2-es fokú. Ezeket 2reguláris gráfoknak nevezzük.
Teljes gráf
Egy egyszerű gráfot, amelynek ‘n’ kölcsönös csúcsa van, teljes gráfnak nevezzük, és ‘Kn’-val jelöljük. A gráfban egy csúcsnak élekkel kell rendelkeznie az összes többi csúccsal, akkor nevezzük teljes gráfnak.
Más szóval, ha egy csúcs kapcsolatban van a gráf összes többi csúcsával, akkor teljes gráfnak nevezzük.
Példa
A következő gráfokban a gráf minden egyes csúcsa kapcsolatban van a gráf összes többi csúcsával, kivéve önmagát.
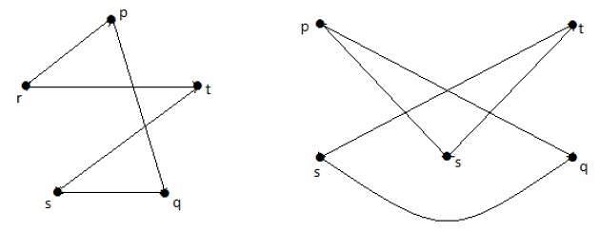
Az I. gráfban,
| a | b | c | |
|---|---|---|---|
| a | Nem kapcsolódik | Connected | Connected |
| b | Connected | Not Connected | Connected |
| c | Connected | Connected | Not Connected |
A grafikon II,
| p | q | r | s | |||
|---|---|---|---|---|---|---|
| p | Nem kapcsolódik | Connected | Connected | Connected | Connected | |
| q | Connected | Not Connected | Connected | Connected | Connected | |
| r | Connected | Kapcsolva | Nem kapcsolódik | Kapcsolva | ||
| s | Kapcsolva | Kapcsolva | Kapcsolva | Kapcsolva | Kapcsolva | Nem Összekapcsolt |
Ciklusgráf
Az ‘n’ csúcsú (n >= 3) és ‘n’ élű egyszerű gráfot ciklusgráfnak nevezzük, ha minden éle ‘n’ hosszúságú ciklust alkot.
Ha a gráf minden egyes csúcsának a foka kettő, akkor ciklikus gráfnak nevezzük.
Notáció – Cn
Példa
Nézzük meg a következő gráfokat –
-
Az I. gráfnak 3 csúcsa van 3 éllel, amelyek egy ‘ab-bc-ca’ ciklust alkotnak.
-
A II. gráfnak 4 csúcsa van 4 éllel, amely egy ‘pq-qs-sr-rp’ ciklust alkot.
-
A III. gráfnak 5 csúcsa van 5 éllel, amely egy ‘ik-km-ml-lj-ji’ ciklust alkot.
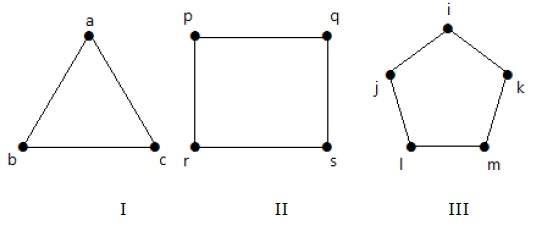
Az összes megadott gráf tehát ciklusgráf.
Kerékgráf
A Cn-1 ciklusgráfból egy új csúcs hozzáadásával kapunk egy kerékgráfot. Ezt az új csúcsot csomópontnak nevezzük, amely a Cn összes csúcsához kapcsolódik.
Notáció – Wn
No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)
Példa
Nézzük meg a következő gráfokat. Ezek mind kerékgráfok.
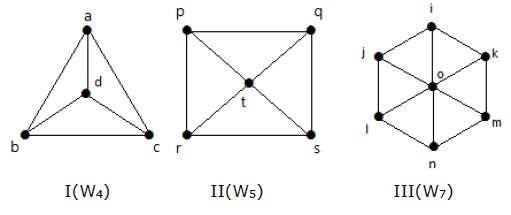
Az I. gráfot a C3-ból úgy kapjuk, hogy a közepén hozzáadunk egy “d” nevű csúcsot. Ezt a gráfot W4-nek nevezzük.
Number of edges in W4 = 2(n-1) = 2(3) = 6
A II. gráf a C4-ből származik, ha a közepén egy ‘t’ nevű csúcsot adunk hozzá. W5.
Number of edges in W5 = 2(n-1) = 2(4) = 8
A III. gráfban a C6-ból úgy kapjuk meg, hogy a közepén egy “o” nevű csúcsot adunk hozzá. Ezt jelöljük W7-nek.
Number of edges in W4 = 2(n-1) = 2(6) = 12
Ciklikus gráf
A legalább egy ciklussal rendelkező gráfot ciklikus gráfnak nevezzük.
Példa
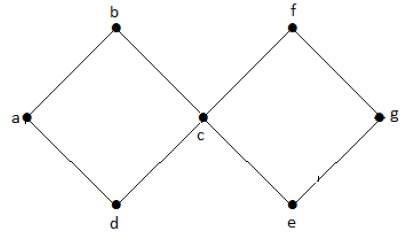
A fenti példagráfban két ciklusunk van a-b-c-d-a és c-f-g-e-c. Ezért ciklikus gráfnak nevezzük.
Aciklikus gráf
A ciklust nem tartalmazó gráfot aciklikus gráfnak nevezzük.
Példa
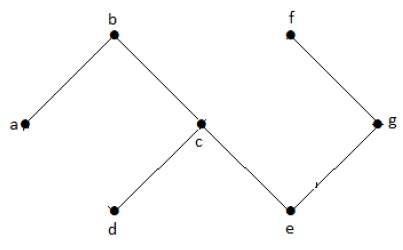
A fenti példagráfban nincsenek ciklusaink. Ezért ez egy nem ciklikus gráf.
Bipartit gráf
Egy egyszerű gráfot G = (V, E) V = {V1, V2} csúcsfelosztással akkor nevezünk bipartit gráfnak, ha E minden éle a V1 egy csúcsát a V2 egy csúcsával köti össze.
A bipertit gráfnak általában két csúcshalmaza van, mondjuk, V1 és V2, és ha egy él rajzolódik, akkor annak a V1 halmaz bármelyik csúcsát a V2 halmaz bármelyik csúcsával össze kell kötnie.
Példa
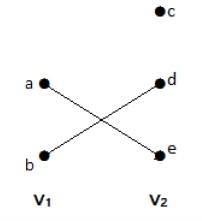
Ebben a gráfban két csúcshalmaz – V1 és V2 – figyelhető meg. Itt két ‘ae’ és ‘bd’ nevű él köti össze a két halmaz V1 és V2 csúcsait.
Teljes kétrészes gráf
A ‘G’ kétrészes gráfot, G = (V, E) V = {V1, V2} partícióval teljes kétrészes gráfnak nevezzük, ha a V1 minden csúcsa kapcsolódik a V2 minden csúcsához.
A teljes kétágú gráf általában a V1 halmaz minden egyes csúcsát összeköti a V2 halmaz minden egyes csúcsával.
Példa
A következő gráf teljes kétágú gráf, mert élei a V1 halmaz minden egyes csúcsát összekötik a V2 halmaz minden egyes csúcsával.
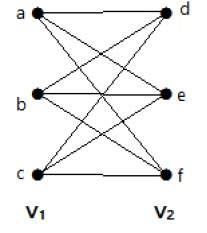
Ha |V1| = m és |V2| = n, akkor a teljes kétágú gráfot Km, n-vel jelöljük.
-
Km,n-nek (m+n) csúcsa és (mn) éle van.
-
Km,n szabályos gráf, ha m=n.
A teljes kétrészes gráf általában nem teljes gráf.
Km,n teljes gráf, ha m=n=1.
Az élek maximális száma egy n csúcsú kétrészes gráfban
Ha n=10, K5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25
Hasonlóképpen K6, 4=24
K7, 3=21
K8, 2=16
K9, 1=9
Ha n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20
Hasonlóképpen K6, 3=18
K7, 2=14
K8, 1=8
‘G’ kétrészes gráf, ha ‘G’ nem tartalmaz páratlan hosszúságú ciklusokat. A kétrészes gráf speciális esete a csillaggráf.
Sztárgráf
A K1, n-1 alakú teljes kétrészes gráf egy n csúcsú csillaggráf. Egy csillaggráf akkor teljes kétrészes gráf, ha egyetlen csúcs tartozik az egyik halmazba, és az összes többi csúcs a másik halmazba.
Példa
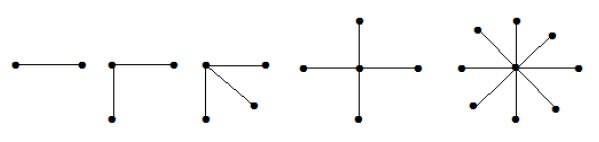
A fenti gráfokban az ‘n’ csúcsból az összes ‘n-1’ csúcs egyetlen csúcshoz kapcsolódik. Ezért K1, n-1 alakúak, amelyek csillaggráfok.
A gráf komplementere
Legyen ‘G-‘ egy egyszerű gráf, amelynek néhány csúcsa olyan, mint ‘G’, és egy él {U, V} jelen van ‘G-‘-ben, ha az él nincs jelen G-ben. Ez azt jelenti, hogy két csúcs szomszédos ‘G-‘-ben, ha a két csúcs nem szomszédos G-ben.
Ha az I gráfban létező élek hiányoznak egy másik, II gráfban, és ha az I és II gráf együttesen egy teljes gráfot alkot, akkor az I és II gráfot egymás komplementerének nevezzük.
Példa
A következő példában az I gráfnak két éle van: ‘cd’ és ‘bd’. A gráf-II komplementjének négy éle van.
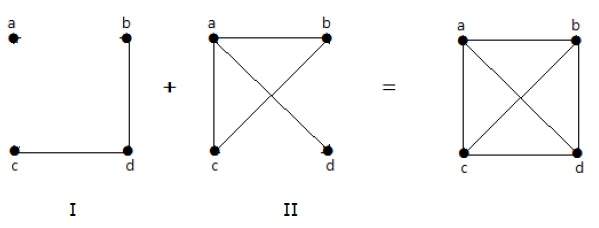
Megjegyezzük, hogy a gráf-I-ben lévő élek nincsenek jelen a gráf-II-ben és fordítva. Ezért a két gráf kombinációja egy ‘n’ csúcsú teljes gráfot ad.
Megjegyzés – Két komplementer gráf kombinációja egy teljes gráfot ad.
Ha ‘G’ bármilyen egyszerű gráf, akkor
|E(G)| + |E(‘G-‘)| = |E(Kn)|, ahol n = a gráf csúcsainak száma.
Példa
Legyen ‘G’ egy egyszerű gráf kilenc csúccsal és tizenkét éllel, találjuk meg az élek számát ‘G-‘-ben.
Megvan, |E(G)| + |E(‘G-‘)| = |E(Kn)|
12 &plusz; |E(‘G-‘)| =
.