Bevezetés
Ez az oldal a folytonossági egyenletet tekinti át, amely a tömeg megőrzését kényszeríti ki az Euler-analízisben. Ez nem szigorúan az anyagi viselkedés leírása, de az így kapott egyenletet gyakran használják azonosságként az anyagi viselkedést leíró konstitutív modellek algebrai manipulálására. Érdemes tehát áttekinteni. A folyadékáramlás elemzésében is központi szerepet játszik, mivel a klasszikus folyadékelemzések nem lehetnek Lagrange-elemzések, mivel az összes folyadékrészecske helyzete \(t = 0\) időpontban ismeretlen.
A tömeg megőrzése
A folytonossági egyenlet azt a tényt tükrözi, hogy a tömeg minden nem nukleáris kontinuummechanikai elemzésben megmarad. Az egyenletet úgy alakítjuk ki, hogy összeadjuk a tömeg be- és kiáramlásának sebességét egy szabályozott térfogatba, és a nettó beáramlást egyenlőre állítjuk a benne lévő tömeg változásának sebességével. Ezt az alábbi ábra szemlélteti.
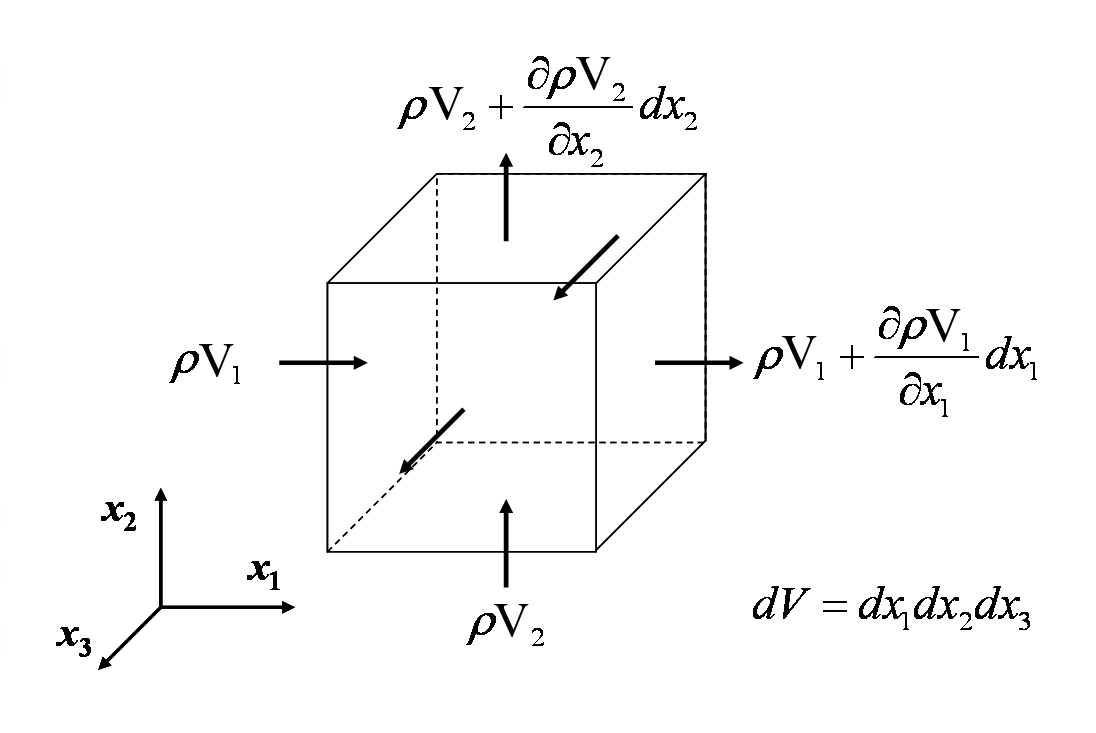
A differenciális szabályozási térfogatba be- és onnan kiáramló összes tömegáramot egyenletbe foglalva megkapjuk
\
A tagok elhagyása és \(dx_1 dx_2 dx_3\) ad
\
és átrendezéssel megkapjuk
\
Ez tömören így írható fel:
\

Fontos pontok
Ezek a véglegesek, teljes és legáltalánosabb formái a tömegmegmaradást érvényesítő folytonossági egyenletnek. Minden anyagra érvényes, nem csak folyadékokra. Tehát szilárd anyagokra is érvényes. Megjegyezzük, hogy ez egyetlen skaláregyenlet, és Euler-egyenlet, mivel a gradienstermek \({\parciális \over \parciális x_i}\), nem pedig \({\parciális \over \parciális X_i}\).
Az a kérdés, hogy van-e Lagrange-egyenlet megfelelője ennek az Euler-egyenletnek. Van. Ezt általában így írják le:
\
Ez egyszerűen azt mondja ki, hogy a tömeg differenciális darabjának a deformált állapotban\(\rho \, dV\) egyenlőnek kell lennie az eredeti értékével\(\rho_o dV_o\) a deformálatlan állapotban.
A folytonossági egyenletnek több speciális esete is van.Az első akkor fordul elő, amikor az áramlás állandósult állapotú. Ebben az esetben az idő szerinti derivált nulla, így marad.
\\
A második speciális eset az összenyomhatatlanság esete, azaz, \(\rho = \)állandó.Ebben az esetben az idő szerinti derivált nulla, és \(\rho\) kivehető az egyenletből, így csak
\
Ez az eredmény elég egyszerű ahhoz, hogy gyakran kibontják.
\
Megjegyezzük, hogy ez nem más, mint \(\text{tr}({\bf D}) = 0\) az összenyomhatatlan anyagok esetében.

Az anyag deriváltja
A következőkre azért érdemes rámutatni, mert lehetővé teszi a sűrűség és a sebességvektor szétválasztását. Az első lépés az, hogy a folytonossági egyenletben lévő divergencia kifejezésre alkalmazzuk a szorzatszabályt.
\
Aztán megjegyezzük, hogy\({\parciális \rho \over \parciális t} + {\bf v} \cdot \nabla \rho\)csak a sűrűség anyagi deriváltja,\({D \rho \over D t}\).
A folytonossági egyenlet tehát így is felírható:
\
Ha az anyag összenyomhatatlan, akkor \(\rho\) nem változhat, tehát\( {D \rho \over D t} \) nullának kell lennie, így marad
\
Az \(\rho\) (mivel nem nulla), így kapjuk
\

Kontinuitási egyenlet példa
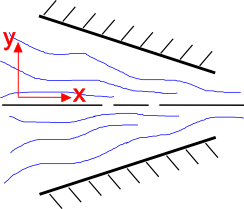
Intuitív, hogy a folyadék áramlása felgyorsul, ahogy a keresztmetszet csökken, ahogy a jobb oldalon látható. A folytonossági egyenlet ezt megmagyarázza. Tekintsük egy összenyomhatatlan folyadék kétdimenziós, állandósult állapotú áramlási mezejét.A folytonossági egyenlet erre a helyzetre a következő
\
Kezdjük az áramlás y-komponensének \(v_2\) vizsgálatával. A konvergáló fúvóka geometriája arra kényszeríti az \(v_2\) komponenst, hogy felfelé áramoljon, ha\(y \lt 0\), és lefelé áramoljon, ha \(y \gt 0\). Tehát \(v_2 \gt 0\), amikor\(y \lt 0\) és \(v_2 \lt 0\), amikor \(y \gt 0\).
Ennek nettó hatása az, hogy \({\parciális v_2 \over \parciális x_2} \lt 0\)a konvergáló fúvókában.
A folytonossági egyenlet azonban azt diktálja, hogy a két részleges derivált összege nulla legyen. Ha tehát a második kisebb, mint nulla, akkor
\
Az pedig azt jelenti, hogy a folyadék áramlásának gyorsulnia kell.