Mint a süteményből is lehet 2 kis darab, vagy 1 kétszer akkora darab, és ugyanannyi. Ezért sok tört egyenértékű, mint például a 2/5 és a 4/10.


Minden szám írható törtként
Minden 1-nél nagyobb egész számot törtnek írunk, hiszen minden osztatlan egészben a részek száma egy.
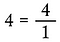
Töredékek szorzása egyenesen keresztben
A törtek szorzása egyszerű, csak szorozzuk egyenesen keresztben.
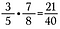
Megjegyzés: A vegyes számokat először helytelen törtekké kell alakítani, erről bővebben itt olvashatsz.
Szorozzuk az 1 bármelyik formájával bármikor
Az 1-es számot multiplikatív azonosságnak nevezzük, mert bármelyik számmal megszorozhatjuk, és a szám ugyanaz marad. Ez azért fontos a törteknél, mert gyakran előfordul, hogy meg kell változtatnunk egy tört megjelenését anélkül, hogy ténylegesen megváltoztatnánk az értékét.
Például az 1/3-at a 3/3-mal való szorzással a 3/9-nek megfelelő törtre tudom változtatni.
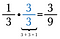
Egyenlő nagyságú részek összeadása és kivonása
A törtek összeadásakor és kivonásakor a nevezőknek azonosnak kell lenniük. Ennek van értelme. Ha egyesíteni vagy elvonni akarunk részeket, akkor azonos méretű részekről kell beszélnünk, különben zavaros lenne a dolog.
Mit teszünk tehát, ha a törtek nem azonos méretűek?
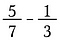
Megszorozzuk egy alakkal, hogy a nevezők közös méretűvé váljanak. Lényegében a törteket kisebb méretű darabokra osztjuk, amíg azonos méretűek nem lesznek. Ezt nevezzük közös nevező megtalálásának.
Igazság szerint bármelyik közös nevező megteszi, de az emberek inkább a legkisebbet keresik. Ebben az esetben a legkisebb szám, amibe mind a 7, mind a 3 maradék nélkül belefér, a 21. Szorozzuk tehát az első törtet 3/3-mal, a másodikat pedig 7/7-gyel.
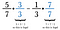
Ha nem jut eszünkbe a legkisebb közös nevező, akkor mindig megszorozhatjuk mindkét törtet az ellenkező nevezővel. Néha, mint ebben az esetben is, kiderül, hogy ez a legkisebb közös nevező. Ha nem az, akkor a végén csak csökkentsd a válaszodat.
Mihelyt a nevezők megegyeznek, vond ki a számlálókat, hogy megkapd a 8/21-et.
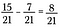
Ez úgy működik, ahogy azt várnánk. Képletesen kezdjük 15 darab 21 darabból összesen.

A 15 kék blokkból 7-ről távolítsuk el a színezést.

Mivel a várakozásnak megfelelően 8/21 marad.
Változtassuk ki először a vegyes számokat
A vegyes szám egy egész szám és egy tört szám kombinációja.
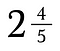
A vegyes számok nem játszanak jól más törtekkel. Érdemes őket először helytelen törtekké alakítani.
Megjegyzés: A helytelen tört olyan tört, amelynek számlálója nagyobb, mint a nevezője, ezért értéke nagyobb, mint egy.
A vegyes szám átalakítása valójában összeadás
A 2 és 4/5 helytelen törté alakításához add össze a 2 + 4/5-öt.
1. lépés: Kezdd azzal, hogy a 2-t átírod 2/1-re.
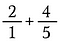
2. lépés: Szorozzuk meg 2/1-et 5/5-tel, hogy egy 10/5-ös egyenértékű törtet kapjunk, amelynek a kívánt közös nevezője 5 lesz.
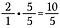
3. lépés: Add össze 10/5 + 4/5.
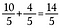
Az eredményünk a 14/5 egyenértékű helytelen tört.
Hogy visszaalakítsuk vegyes számmá, végezzük el az osztást. Például az 5 kétszer 14-be megy (mivel 5 x 2 = 10), és 4 darab marad.
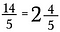
Töredékek összehasonlítása a kereszttétel segítségével
Tegyük fel, hogy meg akarjuk határozni, melyik a nagyobb: 5/12 vagy 6/13.
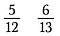
Első lépés: Szorozzuk meg az átlót, és a szorzatot írjuk a számláló fölé.
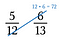
Kettes lépés: Szorozzuk meg a másik átlót, és írjuk a szorzatát a számláló fölé.
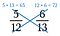
Harmadik lépés: Hasonlítsa össze a termékeket. A nagyobb szorzatú oldal a nagyobb tört. Tehát ebben az esetben 5/12 kisebb, mint 6/13.
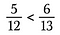
A törtek egyenlőségét a kereszttagok segítségével is megállapíthatjuk.
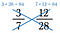
A 3/7 és a 12/28 keresztszáma egyaránt 84, tehát 3/7 = 12/28.
Mindent, ami egybe oszlik
A törtekben az a legjobb, hogy rengeteg lehetőséget találunk a törlésre. Ezáltal gyorsan és könnyen kezelhetővé válnak.
Tegyük fel, hogy megvan a 8/10-es tört. Mind a 8, mind a 10 átírható 2-vel mint tényezővel.
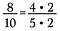
Mivel 2/2 = 1, a 2-eseket ki tudom törölni, így 4/5 marad a redukált tört.
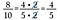
Kihasználom ezt a stratégiát, hogy a törtek szorzását is megkönnyítsem.
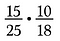
Az egyes számok faktorokba való átírásával kezdjük.
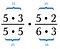
Hagyjuk ki az 1-re osztó számpárokat. Például 5/5 = 1.
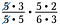
Még egy másik 5-ös számpár, valamint egy 3-as számpár, amelyek szintén 1-gyel osztanak.
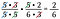
Oops! A 6-ot átírhattam volna 2 x 3-ra, és törölhettem volna egy pár kettest. Nem baj, ha kihagysz egy tényezőt, csak addig folytasd, amíg mindet meg nem kapod.
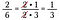
Ha közvetlenül 15/25-ször 10/18-at szoroztam volna meg, az sok számolás lett volna, a törléssel előre lecsökkentem a törteket, és egyszerűbbé teszem a szorzást.
A szorzás használata törtek osztására
A törtek osztásának fogalma egyszerű példákkal, például:

Egy egészben két fél van, tehát 5 egészben 10 fél van.
A fogalom azonban bonyolultabb törtek esetén bonyolulttá válik.
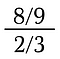
A feladat megoldásához két tényt fogunk felhasználni:
- Az egyes bármelyik formájával szorozhatunk (pl.azaz bármit önmagán felül)
- A 3/2 reciprokával, azaz a 2/3-mal szorozva, a kiiktatáson keresztül 1-et kapunk
Első lépés: Kezdjük a szorzást a reciprokkal önmagán.
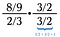
Most már két kisebb problémát kell megoldanunk (kék és zöld).
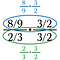
Kettes lépés: Töröljünk ki mindent, ami az alsó (zöld) törtben 1-gyel oszlik. Ennek mindig 1-et kell eredményeznie.

Most már csak a felső feladatot kell megoldanunk.
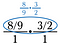
Harmadik lépés: A törléssel előzetesen csökkentsük a törtet. Miután elvégezted ezeket a redukciókat, szorozz át, hogy megkapd a 4/3-at.

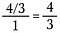
Rövidítés
Ez a “flip and multiply” hosszúkezes mechanikája.”
Az alsó reciprokkal való szorzást kihagyhatjuk, mivel az mindig 1-re törlődik. Ezért csak annyit kell tennünk, hogy a számlálót megszorozzuk a nevező reciprokával.

Bonusz: elmélet, ha esetleg érdekel…
Nagy kérdés! Az általánosításhoz alkossunk két törtet az a, b, c és d betűkkel négy különböző számot jelölve.
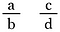
Mindkét törtet szorozzuk meg b-d-vel (így ki tudjuk egyenlíteni a nevezőket).
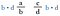
Most töröljük a bal oldali b-t és a jobb oldali d-t, mivel azok 1-gyel osztanak. Már nincsenek törtjeink, csak a d-a és c-b szorzatai.
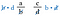
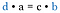
Nézzük vissza az eredeti törteket. Ezek ugyanazok a termékek, mintha az átlósokat szoroztuk volna meg. Ezért a rövidítés az, hogy a kereszttöredéket hasonlítjuk össze.
❤ LENNI KAPCSOLATBAN ❤
Tartsd magad naprakészen mindenben, amiben a Math Hacks készül!