Théorie des graphes – Types de graphes

Il existe différents types de graphes selon le nombre de sommets, le nombre d’arêtes, l’interconnexion et leur structure globale. Nous n’aborderons que quelques types de graphes importants dans ce chapitre.

Graphes nuls

Un graphe n’ayant aucune arête est appelé un graphe nul.

Exemple

Dans le graphe ci-dessus, il y a trois sommets nommés ‘a’, ‘b’ et ‘c’, mais il n’y a aucune arête entre eux. Par conséquent, c’est un graphique nul.

Graphique trivial

Un graphique avec un seul sommet est appelé un graphique trivial.

Exemple

Dans le graphique ci-dessus, il n’y a qu’un seul sommet ‘a’ sans aucune autre arête. C’est donc un graphe trivial.

Graphe non dirigé

Un graphe non dirigé contient des arêtes mais les arêtes ne sont pas dirigées.

Exemple

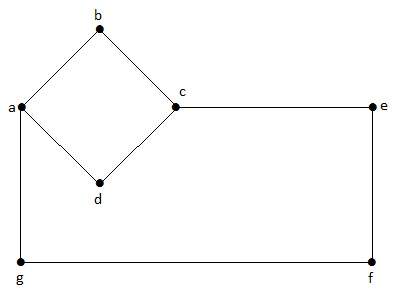
Dans ce graphe, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’ sont les sommets, et ‘ab’, ‘bc’, ‘cd’, ‘da’, ‘ag’, ‘gf’, ‘ef’ sont les arêtes du graphe. Comme il s’agit d’un graphe non dirigé, les arêtes ‘ab’ et ‘ba’ sont identiques. Les autres arêtes sont également considérées de la même manière.

Graphe dirigé

Dans un graphe dirigé, chaque arête a une direction.

Exemple

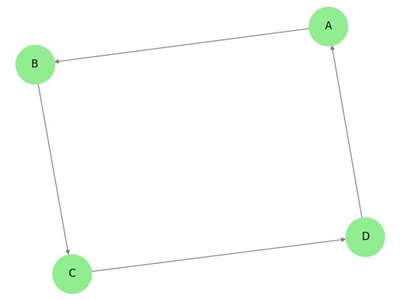
Dans le graphe ci-dessus, nous avons sept sommets ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, et ‘g’, et huit arêtes ‘ab’, ‘cb’, ‘dc’, ‘ad’, ‘ec’, ‘fe’, ‘gf’, et ‘ga’. Comme il s’agit d’un graphe dirigé, chaque arête porte une flèche qui indique sa direction. Notez que dans un graphe dirigé, ‘ab’ est différent de ‘ba’.

Graphe simple

Un graphe sans boucles et sans arêtes parallèles est appelé un graphe simple.

• Le nombre maximal d’arêtes possibles dans un même graphe à ‘n’ sommets est nC2 où nC2 = n(n – 1)/2.

• Le nombre de graphes simples possibles avec ‘n’ sommets = 2nc2 = 2n(n-1)/2.

Exemple

Dans le graphe suivant, il y a 3 sommets avec 3 arêtes ce qui est le maximum en excluant les arêtes parallèles et les boucles. Ceci peut être prouvé en utilisant les formules ci-dessus.

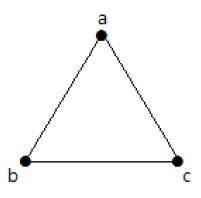
Le nombre maximum d’arêtes avec n=3 sommets –

nC2 = n(n–1)/2 = 3(3–1)/2 = 6/2 = 3 edges

Le nombre maximum de graphes simples avec n=3 sommets –

2nC2 = 2n(n-1)/2 = 23(3-1)/2 = 23 = 8

Ces 8 graphes sont présentés ci-dessous –

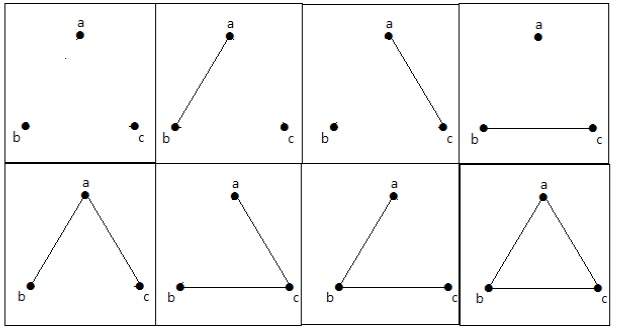
Graphe connecté

Un graphe G est dit connecté s’il existe un chemin entre chaque paire de sommets. Il doit y avoir au moins une arête pour chaque sommet du graphe. De sorte que nous pouvons dire qu’il est connecté à un autre sommet de l’autre côté de l’arête.

Exemple

Dans le graphe suivant, chaque sommet a sa propre arête connectée à une autre arête. Par conséquent, c’est un graphe connecté.

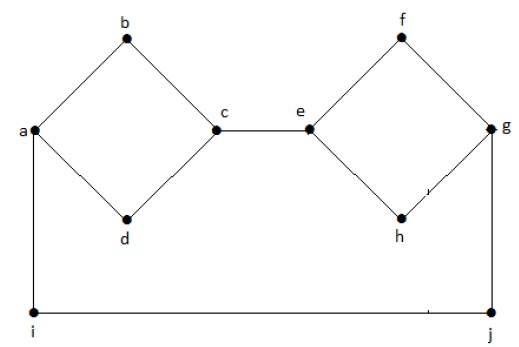
Graphe déconnecté

Un graphe G est déconnecté, s’il ne contient pas au moins deux sommets connectés.

Exemple 1

Le graphe suivant est un exemple de graphe déconnecté, où il y a deux composantes, l’une avec des sommets ‘a’, ‘b’, ‘c’, ‘d’ et l’autre avec des sommets ‘e’, ‘f’, ‘g’, ‘h’.

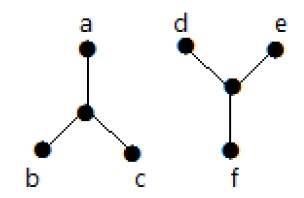
Les deux composantes sont indépendantes et non connectées l’une à l’autre. D’où l’appellation de graphe déconnecté.

Exemple 2

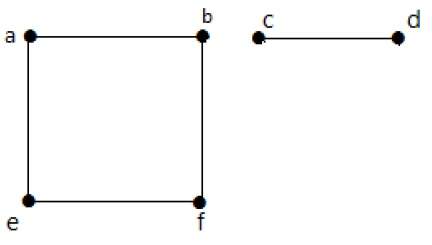
Dans cet exemple, il y a deux composantes indépendantes, a-b-f-e et c-d, qui ne sont pas connectées entre elles. Il s’agit donc d’un graphe déconnecté.

Graphe régulier

Un graphe G est dit régulier, si tous ses sommets ont le même degré. Dans un graphe, si le degré de chaque sommet est ‘k’, alors le graphe est appelé un ‘graphe k-régulier’.

Exemple

Dans les graphes suivants, tous les sommets ont le même degré. Donc ces graphes sont appelés graphes réguliers.

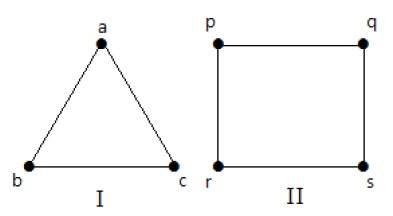
Dans les deux graphes, tous les sommets ont le degré 2. On les appelle des graphes 2-réguliers.

Graphes complets

Un graphe simple avec ‘n’ sommets mutuels est appelé un graphe complet et il est noté par ‘Kn’. Dans le graphe, un sommet doit avoir des arêtes avec tous les autres sommets, alors il est appelé un graphe complet.

En d’autres termes, si un sommet est connecté à tous les autres sommets d’un graphe, alors il est appelé un graphe complet.

Exemple

Dans les graphes suivants, chaque sommet du graphe est connecté avec tous les autres sommets du graphe sauf par lui-même.

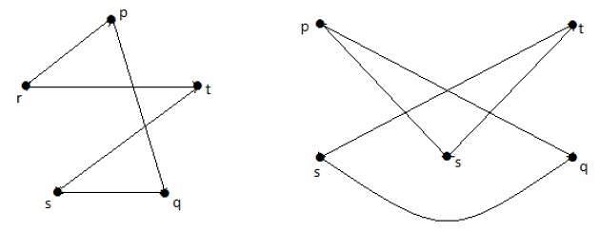
Dans le graphe I,

.

	a	b	c
a	Non connecté	Connecté	Connecté
b	Connecté	Non connecté	Connecté
c	Connecté	Connecté	Non connecté

Dans le graphe II,

.

	p	q	r	s
p	Non connecté	Connecté	Connecté	Connecté	Connecté
q	Connecté	Non connecté	Connecté	Connecté
r	Connecté	Connecté	Non Connecté	Connecté
s	Connecté	Connecté	Connecté	Non Connecté Connecté

Graphe à cycles

Un graphe simple avec ‘n’ sommets (n >= 3) et ‘n’ arêtes est appelé un graphe à cycles si toutes ses arêtes forment un cycle de longueur ‘n’.

Si le degré de chaque sommet du graphe est de deux, alors il est appelé un graphe de cycle.

Notation – Cn

Exemple

Regardez les graphes suivants –

• Le graphe I a 3 sommets avec 3 arêtes qui forment un cycle ‘ab-bc-ca’.

• Le graphe II a 4 sommets avec 4 arêtes qui forment un cycle ‘pq-qs-sr-rp’.

• Le graphe III a 5 sommets avec 5 arêtes qui forment un cycle ‘ik-km-ml-lj-ji’.

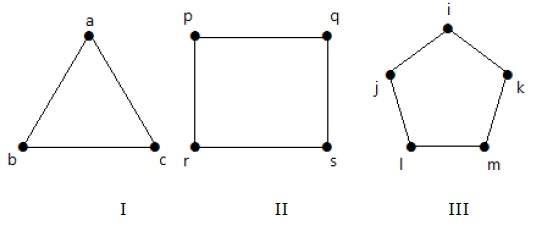
Donc tous les graphes donnés sont des graphes de cycles.

Graphes de roues

Un graphe de roues est obtenu à partir d’un graphe de cycles Cn-1 en ajoutant un nouveau sommet. Ce nouveau sommet est appelé un Hub qui est connecté à tous les sommets de Cn.

Notation – Wn

No. of edges in Wn = No. of edges from hub to all other vertices + No. of edges from all other nodes in cycle graph without a hub. = (n–1) + (n–1) = 2(n–1)

Exemple

Prenez connaissance des graphes suivants. Ce sont tous des graphes de roues.

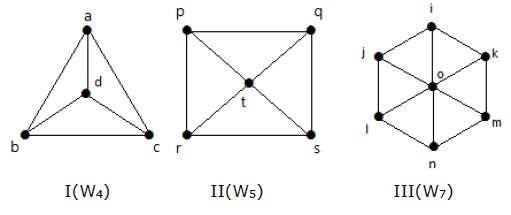
Dans le graphe I, il est obtenu à partir de C3 en ajoutant un sommet au milieu nommé ‘d’. Il est noté W4.

Number of edges in W4 = 2(n-1) = 2(3) = 6

Dans le graphe II, il est obtenu à partir de C4 en ajoutant un sommet au milieu nommé ‘t’. Il est noté W5.

Number of edges in W5 = 2(n-1) = 2(4) = 8

Dans le graphe III, il est obtenu à partir de C6 en ajoutant un sommet au milieu nommé ‘o’. Il est noté W7.

Number of edges in W4 = 2(n-1) = 2(6) = 12

Graphe cyclique

Un graphe avec au moins un cycle est appelé un graphe cyclique.

Exemple

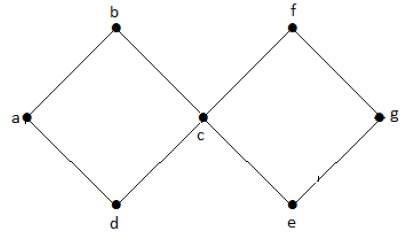
Dans l’exemple de graphe ci-dessus, nous avons deux cycles a-b-c-d-a et c-f-g-e-c. Par conséquent, on l’appelle un graphe cyclique.

Graphe acyclique

Un graphe sans cycles est appelé un graphe acyclique.

Exemple

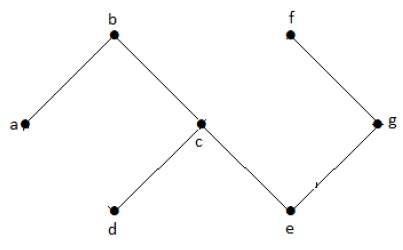
Dans l’exemple de graphe ci-dessus, nous n’avons pas de cycles. Par conséquent, c’est un graphe non-cyclique.

Graphe biparti

Un graphe simple G = (V, E) avec une partition de sommets V = {V1, V2} est appelé graphe biparti si chaque arête de E joint un sommet dans V1 à un sommet dans V2.

En général, un graphe Bipertite a deux ensembles de sommets, disons, V1 et V2, et si une arête est dessinée, elle doit relier tout sommet de l’ensemble V1 à tout sommet de l’ensemble V2.

Exemple

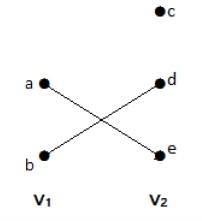
Dans ce graphe, vous pouvez observer deux ensembles de sommets – V1 et V2. Ici, deux arêtes nommées ‘ae’ et ‘bd’ relient les sommets de deux ensembles V1 et V2.

Graphe biparti complet

Un graphe biparti ‘G’, G = (V, E) avec la partition V = {V1, V2} est dit être un graphe biparti complet si chaque sommet de V1 est relié à chaque sommet de V2.

En général, un graphe biparti complet relie chaque sommet de l’ensemble V1 à chaque sommet de l’ensemble V2.

Exemple

Le graphe suivant est un graphe biparti complet car il possède des arêtes reliant chaque sommet de l’ensemble V1 à chaque sommet de l’ensemble V2.

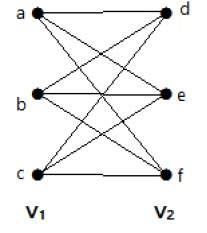
Si |V1| = m et |V2| = n, alors le graphe biparti complet est noté Km, n.

• Km,n a (m+n) sommets et (mn) arêtes.

• Km,n est un graphe régulier si m=n.

En général, un graphe biparti complet n’est pas un graphe complet.

Km,n est un graphe complet si m=n=1.

Le nombre maximal d’arêtes dans un graphe biparti à n sommets est

Si n=10, k5, 5= ⌊n2/4⌋ = ⌊102/4⌋ = 25

De même K6, 4=24

K7, 3=21

K8, 2=16

K9, 1=9

Si n=9, k5, 4 = ⌊n2/4⌋ = ⌊92/4⌋ = 20

Similairement K6, 3=18

K7, 2=14

K8, 1=8

‘G’ est un graphe bipartite si ‘G’ n’a pas de cycles de longueur impaire. Un cas particulier de graphe bipartite est un graphe en étoile.

Graphe en étoile

Un graphe bipartite complet de la forme K1, n-1 est un graphe en étoile à n sommets. Un graphe en étoile est un graphe biparti complet si un seul sommet appartient à un ensemble et que tous les autres sommets appartiennent à l’autre ensemble.

Exemple

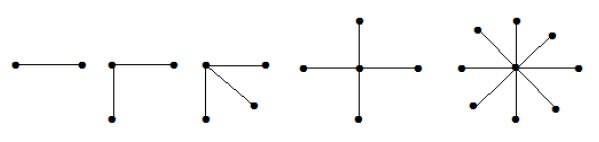
Dans les graphes ci-dessus, sur ‘n’ sommets, tous les ‘n-1’ sommets sont reliés à un seul sommet. Par conséquent, il est sous la forme de K1, n-1 qui sont des graphes en étoile.

Complément d’un graphe

Laissons ‘G-‘ être un graphe simple avec certains sommets comme celui de ‘G’ et une arête {U, V} est présente dans ‘G-‘, si l’arête n’est pas présente dans G. Cela signifie que deux sommets sont adjacents dans ‘G-‘ si les deux sommets ne sont pas adjacents dans G.

Si les arêtes qui existent dans le graphe I sont absentes dans un autre graphe II, et si le graphe I et le graphe II sont combinés ensemble pour former un graphe complet, alors le graphe I et le graphe II sont appelés compléments l’un de l’autre.

Exemple

Dans l’exemple suivant, le graphe-I a deux arêtes ‘cd’ et ‘bd’. Son complément le graphe-II a quatre arêtes.

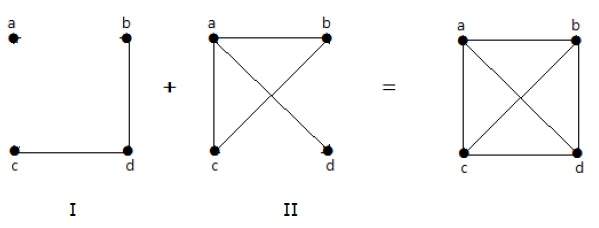
Notez que les arêtes du graphe-I ne sont pas présentes dans le graphe-II et vice versa. Par conséquent, la combinaison des deux graphes donne un graphe complet de ‘n’ sommets.

Note – Une combinaison de deux graphes complémentaires donne un graphe complet.

Si ‘G’ est un graphe simple quelconque, alors

|E(G)| + |E(‘G-‘)| = |E(Kn)|, où n = nombre de sommets dans le graphe.

Exemple

Si ‘G’ est un graphe simple avec neuf sommets et douze arêtes, trouvez le nombre d’arêtes dans ‘G-‘.

Vous avez, |E(G)| + |E(‘G-‘)| = |E(Kn)|

12 &plus ; |E(‘G-‘)| =

.