Lorsque les données sont prêtes à être analysées, il convient d’évaluer de manière approfondie, sur la base de l’inspection des données, si des méthodes statistiques doivent être utilisées pour traiter les données manquantes. Bell et al. ont cherché à évaluer l’étendue et le traitement des données manquantes dans les essais cliniques randomisés publiés entre juillet et décembre 2013 dans le BMJ, le JAMA, le Lancet et le New England Journal of Medicine . 95 % des 77 essais identifiés ont signalé des données de résultats manquantes. La méthode la plus couramment utilisée pour traiter les données manquantes dans l’analyse primaire était l’analyse de cas complet (45%), l’imputation simple (27%), les méthodes basées sur un modèle (par exemple, les modèles mixtes ou les équations d’estimation généralisées) (19%) et l’imputation multiple (8%) .
Analyse de cas complet
L’analyse de cas complet est une analyse statistique basée sur les participants avec un ensemble complet de données sur les résultats. Les participants avec toute donnée manquante sont exclus de l’analyse. Comme décrit dans l’introduction, si les données manquantes sont MCAR, l’analyse de cas complète aura une puissance statistique réduite en raison de la taille réduite de l’échantillon, mais les données observées ne seront pas biaisées . Lorsque les données manquantes ne sont pas des MCAR, l’estimation de l’effet de l’intervention par l’analyse de cas complète peut être fondée, c’est-à-dire qu’il y aura souvent un risque de surestimation des avantages et de sous-estimation des inconvénients. Veuillez consulter la section » Faut-il utiliser l’imputation multiple pour traiter les données manquantes ? » pour une discussion plus détaillée de la validité potentielle si l’analyse de cas complète est appliquée.
Imputation simple
Lorsque l’on utilise l’imputation simple, les valeurs manquantes sont remplacées par une valeur définie par une certaine règle . Il existe de nombreuses formes d’imputation simple, par exemple, la dernière observation reportée (les valeurs manquantes d’un participant sont remplacées par la dernière valeur observée du participant), la pire observation reportée (les valeurs manquantes d’un participant sont remplacées par la pire valeur observée du participant) et l’imputation moyenne simple . Dans l’imputation par moyenne simple, les valeurs manquantes sont remplacées par la moyenne de cette variable . L’utilisation de l’imputation simple entraîne souvent une sous-estimation de la variabilité, car chaque valeur non observée a le même poids dans l’analyse que les valeurs observées connues. La validité de l’imputation simple ne dépend pas du fait que les données soient MCAR ou non ; l’imputation simple dépend plutôt d’hypothèses spécifiques selon lesquelles les valeurs manquantes, par exemple, sont identiques à la dernière valeur observée . Ces hypothèses sont souvent irréalistes et l’imputation simple est donc souvent une méthode potentiellement biaisée et doit être utilisée avec une grande prudence .
L’imputation multiple
L’imputation multiple s’est avérée être une méthode générale valide pour traiter les données manquantes dans les essais cliniques randomisés, et cette méthode est disponible pour la plupart des types de données . Nous décrirons dans les sections suivantes quand et comment l’imputation multiple doit être utilisée.
L’imputation multiple doit-elle être utilisée pour traiter les données manquantes ?
Raisons pour lesquelles l’imputation multiple ne doit pas être utilisée pour traiter les données manquantes
Est-il valable d’ignorer les données manquantes ?
L’analyse des données observées (analyse des cas complets) en ignorant les données manquantes est une solution valable dans trois circonstances .
- a)
L’analyse de cas complets peut être utilisée comme analyse primaire si les proportions de données manquantes sont inférieures à environ 5% (en règle générale) et s’il est peu plausible que certains groupes de patients (par exemple, les participants très malades ou très « bien portants ») soient spécifiquement perdus de vue dans l’un des groupes comparés . En d’autres termes, si l’impact potentiel des données manquantes est négligeable, celles-ci peuvent être ignorées dans l’analyse. En cas de doute, il est possible d’utiliser les analyses de sensibilité du meilleur et du pire des cas : on génère d’abord un ensemble de données du scénario du « meilleur et du pire des cas » où l’on suppose que tous les participants perdus de vue dans un groupe (appelé groupe 1) ont eu un résultat bénéfique (par exemple, n’ont pas eu d’événement indésirable grave) et que tous ceux dont les résultats sont manquants dans l’autre groupe (groupe 2) ont eu un résultat néfaste (par exemple, ont eu un événement indésirable grave). Ensuite, un ensemble de données du scénario le plus défavorable est généré, où l’on suppose que tous les participants perdus au suivi dans le groupe 1 ont eu un résultat néfaste et que tous ceux perdus au suivi dans le groupe 2 ont eu un résultat bénéfique. Si des résultats continus sont utilisés, un « résultat bénéfique » peut être la moyenne du groupe plus 2 écarts types (ou 1 écart type) de la moyenne du groupe, et un « résultat néfaste » peut être la moyenne du groupe moins 2 écarts types (ou 1 écart type) de la moyenne du groupe. Pour les données dichotomisées, ces analyses de sensibilité du meilleur et du pire des cas montreront alors la plage d’incertitude due aux données manquantes, et si cette plage ne donne pas de résultats qualitativement contradictoires, alors les données manquantes peuvent être ignorées. Pour les données continues, l’imputation avec 2 SD représentera une plage possible d’incertitude étant donné 95 % des données observées (si elles sont normalement distribuées).
- b)
Si seule la variable dépendante a des valeurs manquantes et que les variables auxiliaires (variables non incluses dans l’analyse de régression, mais corrélées avec une variable ayant des valeurs manquantes et/ou liées à son caractère manquant) ne sont pas identifiées, l’analyse de cas complète peut être utilisée comme analyse primaire et aucune méthode spécifique ne doit être utilisée pour traiter les données manquantes . Aucune information supplémentaire ne sera obtenue, par exemple, en utilisant l’imputation multiple, mais les erreurs standard peuvent augmenter en raison de l’incertitude introduite par l’imputation multiple .
- c)
Comme mentionné ci-dessus (voir Méthodes de traitement des données manquantes), il serait également valable de simplement effectuer une analyse de cas complet s’il est relativement certain que les données sont MCAR (voir Introduction). Il est relativement rare que l’on soit certain que les données sont MCAR. Il est possible de tester l’hypothèse selon laquelle les données sont MCAR à l’aide du test de Little, mais il peut être imprudent de s’appuyer sur des tests qui se sont révélés non significatifs. Par conséquent, s’il existe un doute raisonnable sur le fait que les données sont MCAR, même si le test de Little n’est pas significatif (ne parvient pas à rejeter l’hypothèse nulle selon laquelle les données sont MCAR), il ne faut pas supposer que les données sont MCAR.
Les proportions de données manquantes sont-elles trop importantes ?
Si de grandes proportions de données sont manquantes, il faudrait envisager de rapporter simplement les résultats de l’analyse complète des cas, puis discuter clairement des limites interprétatives qui en résultent pour les résultats de l’essai. Si des imputations multiples ou d’autres méthodes sont utilisées pour traiter les données manquantes, cela pourrait indiquer que les résultats de l’essai sont confirmatifs, ce qui n’est pas le cas si les données manquantes sont considérables. Si les proportions de données manquantes sont très importantes (par exemple, plus de 40 %) sur des variables importantes, alors les résultats de l’essai ne peuvent être considérés que comme des résultats générateurs d’hypothèses . Une exception rare serait si le mécanisme sous-jacent derrière les données manquantes peut être décrit comme MCAR (voir paragraphe ci-dessus).
L’hypothèse MCAR et l’hypothèse MAR semblent-elles toutes deux peu plausibles ?
Si l’hypothèse MAR semble peu plausible sur la base des caractéristiques des données manquantes, alors les résultats de l’essai risquent d’être biaisés en raison du « biais des données de résultats incomplètes » et aucune méthode statistique ne peut avec certitude tenir compte de ce biais potentiel . La validité des méthodes utilisées pour traiter les données MNAR nécessite certaines hypothèses qui ne peuvent être testées sur la base des données observées. Les analyses de sensibilité du meilleur et du pire des cas peuvent montrer toute la gamme théorique d’incertitude et les conclusions doivent être liées à cette gamme d’incertitude. Les limites des analyses doivent être discutées et prises en compte de manière approfondie.
La variable de résultat avec valeurs manquantes est-elle continue et le modèle analytique est-il compliqué (par exemple avec des interactions) ?
Dans cette situation, on peut envisager d’utiliser la méthode du maximum de vraisemblance directe pour éviter les problèmes de compatibilité des modèles entre le modèle analytique et le modèle d’imputation multiple lorsque le premier est plus général que le second. En général, les méthodes de maximum de vraisemblance directe peuvent être utilisées, mais à notre connaissance, les méthodes disponibles dans le commerce ne sont actuellement disponibles que pour les variables continues.
Quand et comment utiliser les imputations multiples
Si aucune des « Raisons pour lesquelles l’imputation multiple ne devrait pas être utilisée pour traiter les données manquantes » ci-dessus n’est remplie, alors l’imputation multiple pourrait être utilisée. Diverses procédures ont été proposées dans la littérature au cours des dernières décennies pour traiter les données manquantes . Nous avons exposé les considérations susmentionnées des méthodes statistiques pour traiter les données manquantes dans la Fig. 1.
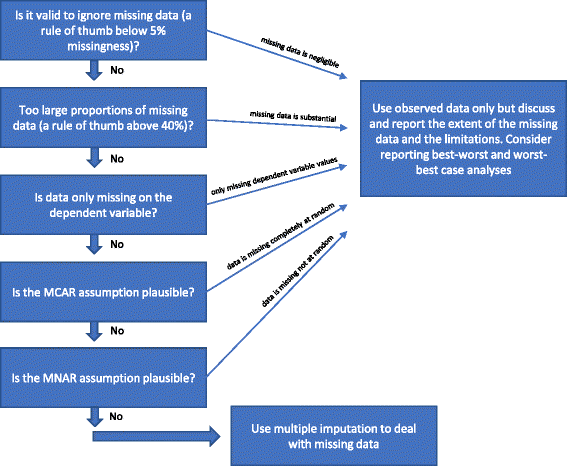
Diagramme de flux : quand faut-il utiliser l’imputation multiple pour traiter les données manquantes lors de l’analyse des résultats des essais cliniques randomisés
L’imputation multiple a vu le jour au début des années 1970 et a gagné en popularité au fil des ans . L’imputation multiple est une technique statistique basée sur la simulation pour traiter les données manquantes . L’imputation multiple comprend trois étapes :
-
Étape d’imputation. Une » imputation » représente généralement un ensemble de valeurs plausibles pour les données manquantes – l’imputation multiple représente plusieurs ensembles de valeurs plausibles . Lorsqu’on utilise l’imputation multiple, les valeurs manquantes sont identifiées et remplacées par un échantillon aléatoire d’imputations de valeurs plausibles (ensembles de données complets). De multiples ensembles de données complétés sont générés par un modèle d’imputation choisi. Cinq ensembles de données imputées ont traditionnellement été suggérés comme suffisants pour des raisons théoriques, mais 50 ensembles de données (ou plus) semblent préférables pour réduire la variabilité d’échantillonnage du processus d’imputation .
-
Étape d’analyse (estimation) des données complétées. L’analyse souhaitée est effectuée séparément pour chaque ensemble de données qui est généré pendant l’étape d’imputation . Ainsi, par exemple, 50 résultats d’analyse sont construits.
-
Étape de mise en commun. Les résultats obtenus à partir de chaque analyse de données complétées sont combinés en un seul résultat d’imputation multiple . Il n’est pas nécessaire d’effectuer une méta-analyse pondérée car tous les résultats d’analyse disons 50 sont considérés comme ayant le même poids statistique.
Il est très important qu’il y ait soit une compatibilité entre le modèle d’imputation et le modèle d’analyse, soit que le modèle d’imputation soit plus général que le modèle d’analyse (par exemple, que le modèle d’imputation comprenne plus de covariables indépendantes que le modèle d’analyse) . Par exemple, si le modèle d’analyse comporte des interactions significatives, alors le modèle d’imputation doit les inclure également , si le modèle d’analyse utilise une version transformée d’une variable alors le modèle d’imputation doit utiliser la même transformation , etc.
Différents types d’imputation multiple
Différents types de méthodes d’imputation multiple existent. Nous les présenterons selon leur degré croissant de complexité : 1) analyse de régression à valeur unique ; 2) imputation monotone ; 3) équations enchaînées ou méthode de Monte Carlo à chaîne de Markov (MCMC). Nous allons dans les paragraphes suivants décrire ces différentes méthodes d’imputation multiple et comment choisir entre elles.
Une analyse de régression à valeur unique comprend une variable dépendante et les variables de stratification utilisées dans la randomisation. Les variables de stratification comprennent souvent un indicateur de centre si l’essai est multicentrique et généralement une ou plusieurs variables d’ajustement avec des informations pronostiques qui sont corrélées avec le résultat. Lorsqu’on utilise une variable dépendante continue, on peut également inclure une valeur de base de la variable dépendante. Comme mentionné dans la section « Raisons pour lesquelles les méthodes statistiques ne doivent pas être utilisées pour traiter les données manquantes », si seule la variable dépendante a des valeurs manquantes et que les variables auxiliaires ne sont pas identifiées, une analyse complète du cas doit être effectuée et aucune méthode spécifique ne doit être utilisée pour traiter les données manquantes. Si des variables auxiliaires ont été identifiées, une imputation à une seule variable peut être effectuée. S’il y a des manques importants sur la variable de base d’une variable continue, une analyse de cas complète peut fournir des résultats biaisés . Par conséquent, dans tous les cas, une imputation à variable unique (avec ou sans variables auxiliaires incluses selon le cas) est effectuée si seule la variable de base est manquante.
Si la variable dépendante et la variable de base sont toutes deux manquantes et que la manquance est monotone, une imputation monotone est effectuée. Supposons une matrice de données où les patients sont représentés par des lignes et les variables par des colonnes. Le caractère manquant d’une telle matrice de données est dit monotone si ses colonnes peuvent être réorganisées de telle sorte que pour tout patient (a) si une valeur est manquante, toutes les valeurs à droite de sa position sont également manquantes, et (b) si une valeur est observée, toutes les valeurs à gauche de cette valeur sont également observées. Si l’absence de données est monotone, la méthode d’imputation multiple est également relativement simple, même si plusieurs variables présentent des valeurs manquantes. Dans ce cas, il est relativement simple d’imputer les données manquantes en utilisant l’imputation par régression séquentielle où les valeurs manquantes sont imputées pour chaque variable à la fois . De nombreux progiciels statistiques (par exemple, STATA) peuvent analyser si le caractère manquant est monotone ou non.
Si le caractère manquant n’est pas monotone, une imputation multiple est réalisée en utilisant les équations chaînées ou la méthode MCMC. Les variables auxiliaires sont incluses dans le modèle si elles sont disponibles. Nous avons résumé comment choisir entre les différentes méthodes d’imputation multiple dans la Fig. 2.
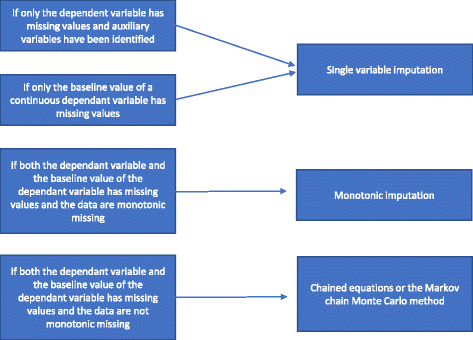
Flowchart de l’imputation multiple
Vraisemblance maximale à information complète
La vraisemblance maximale à information complète est une méthode alternative pour traiter les données manquantes . Le principe de l’estimation du maximum de vraisemblance consiste à estimer les paramètres de la distribution conjointe du résultat (Y) et des covariables (X1,…, Xk) qui, s’ils étaient vrais, maximiseraient la probabilité d’observer les valeurs que nous avons effectivement observées . Si des valeurs manquent chez un patient donné, nous pouvons obtenir la vraisemblance en additionnant la vraisemblance habituelle sur toutes les valeurs possibles des données manquantes, à condition que le mécanisme des données manquantes soit ignorable. Cette méthode est appelée maximum de vraisemblance à information complète.
Le maximum de vraisemblance à information complète présente des points forts et des limites par rapport à l’imputation multiple.
Points forts du maximum de vraisemblance à information complète par rapport à l’imputation multiple
- 1)
Il est plus simple à mettre en œuvre, c’est-à-dire. il n’est pas nécessaire de passer par différentes étapes comme lors de l’utilisation de l’imputation multiple.
- 2)
Contrairement à l’imputation multiple, le maximum de vraisemblance à information complète ne présente aucun problème potentiel d’incompatibilité entre le modèle d’imputation et le modèle d’analyse (voir ‘Imputation multiple’). La validité des résultats de l’imputation multiple sera discutable s’il existe une incompatibilité entre le modèle d’imputation et le modèle d’analyse, ou si le modèle d’imputation est moins général que le modèle d’analyse .
- 3)
Lorsqu’on utilise l’imputation multiple, toutes les valeurs manquantes dans chaque ensemble de données généré (étape d’imputation) sont remplacées par un échantillon aléatoire de valeurs plausibles . Par conséquent, à moins que « une graine aléatoire » ne soit spécifiée, chaque fois qu’une analyse d’imputation multiple est effectuée, des résultats différents seront affichés . Les analyses utilisant le maximum de vraisemblance à information complète sur le même ensemble de données produiront les mêmes résultats chaque fois que l’analyse sera effectuée, et les résultats ne dépendent donc pas d’une graine aléatoire. Cependant, si la valeur de la graine aléatoire est définie dans le plan d’analyse statistique, ce problème peut être résolu.
Limitations de la vraisemblance maximale d’information complète par rapport à l’imputation multiple
Les limitations de l’utilisation de la vraisemblance maximale d’information complète par rapport à l’utilisation de l’imputation multiple, est que l’utilisation de la vraisemblance maximale d’information complète n’est possible qu’en utilisant un logiciel spécialement conçu . Des logiciels préliminaires conçus ont été développés, mais la plupart d’entre eux n’ont pas les caractéristiques des logiciels statistiques conçus commercialement (par exemple, STATA, SAS ou SPSS). Dans STATA (à l’aide de la commande SEM) et SAS (à l’aide de la commande PROC CALIS), il est possible d’utiliser le maximum de vraisemblance à information complète, mais uniquement lorsque l’on utilise des variables dépendantes (résultats) continues. Pour la régression logistique et la régression de Cox, le seul progiciel commercial qui fournit un maximum de vraisemblance à information complète pour les données manquantes est Mplus.
Une autre limitation potentielle lors de l’utilisation du maximum de vraisemblance à information complète est qu’il peut y avoir une hypothèse sous-jacente de normalité multivariée . Néanmoins, les violations de l’hypothèse de normalité multivariée peuvent ne pas être si importantes, de sorte qu’il pourrait être acceptable d’inclure des variables indépendantes binaires dans l’analyse.
Nous avons dans le fichier supplémentaire 1 inclus un programme (SAS) qui produit un ensemble complet de données de jouets, y compris plusieurs analyses différentes de ces données. Le tableau 1 et le tableau 2 montrent la sortie et comment différentes méthodes qui traitent les données manquantes produisent des résultats différents.
Analyse de régression des valeurs du panel
Les données du panel sont généralement contenues dans un fichier de données dit large où la première ligne contient les noms des variables, et les lignes suivantes (une pour chaque patient) contiennent les valeurs correspondantes. Le résultat est représenté par différentes variables – une pour chaque mesure planifiée et chronométrée du résultat. Pour analyser les données, il faut convertir le fichier en un fichier dit long, avec un enregistrement par mesure planifiée de l’issue, comprenant la valeur de l’issue, l’heure de la mesure et une copie de toutes les autres valeurs de variables, à l’exception de celles de la variable d’issue. Pour conserver les corrélations intra-patient entre les mesures de résultats chronométrées, il est courant d’effectuer une impression multiple du fichier de données dans sa forme large, suivie d’une analyse du fichier résultant après qu’il ait été converti dans sa forme longue. On peut utiliser Proc mixed (SAS 9.4) pour l’analyse des valeurs de résultat continues et proc. glimmix (SAS 9.4) pour les autres types de résultats. Comme ces procédures appliquent la méthode directe du maximum de vraisemblance sur les données de résultats, mais ignorent les cas où les valeurs des covariables sont manquantes, elles peuvent être utilisées directement lorsque seules les valeurs de la variable dépendante sont manquantes et qu’aucune bonne variable auxiliaire n’est disponible. Sinon, il convient d’utiliser proc. mixed ou proc. glimmix (selon le cas) après une imputation multiple. De toute évidence, une approche correspondante peut être possible en utilisant d’autres progiciels statistiques.
Analyses de sensibilité
Les analyses de sensibilité peuvent être définies comme un ensemble d’analyses où les données sont traitées d’une manière différente par rapport à l’analyse primaire. Les analyses de sensibilité peuvent montrer comment des hypothèses, différentes de celles faites dans l’analyse primaire, influencent les résultats obtenus . L’analyse de sensibilité doit être prédéfinie et décrite dans le plan d’analyse statistique, mais des analyses de sensibilité post hoc supplémentaires peuvent être justifiées et valables. Lorsque l’influence potentielle des valeurs manquantes n’est pas claire, nous recommandons les analyses de sensibilité suivantes :
-
Nous avons déjà décrit l’utilisation des analyses de sensibilité best-worst et worst-best case pour montrer la plage d’incertitude due aux données manquantes (voir Évaluation de l’opportunité d’utiliser des méthodes pour traiter les données manquantes). Notre description précédente des analyses de sensibilité du meilleur et du pire cas était liée aux données manquantes sur une variable dépendante dichotomique ou continue, mais ces analyses de sensibilité peuvent également être utilisées lorsque des données manquent sur les variables de stratification, les valeurs de base, etc. L’influence potentielle des données manquantes doit être évaluée pour chaque variable séparément, c’est-à-dire qu’il doit y avoir un meilleur scénario et un pire scénario pour chaque variable (variable dépendante, indicateur de résultat et variables de stratification) avec des données manquantes.
-
S’il est décidé que, par exemple, des imputations multiples doivent être utilisées, alors ces résultats doivent être le résultat primaire du résultat donné. Chaque analyse de régression primaire doit toujours être complétée par une analyse de cas observés (ou disponibles) correspondante.
Lorsque des méthodes à effets mixtes sont utilisées
L’utilisation d’un plan d’essai multicentrique sera souvent nécessaire pour recruter un nombre suffisant de participants à l’essai dans un délai raisonnable . Une conception d’essai multicentrique fournit également une meilleure base pour la généralisation ultérieure de ses résultats. Il a été démontré que les méthodes d’analyse les plus couramment utilisées dans les essais cliniques randomisés donnent de bons résultats avec un petit nombre de centres (analyse de résultats dépendants binaires) . Avec un nombre relativement important de centres (50 ou plus), il est souvent optimal d’utiliser le « centre » comme effet aléatoire et d’utiliser des méthodes d’analyse à effet mixte. Il sera également souvent valable d’utiliser des méthodes d’analyse à effets mixtes lors de l’analyse de données longitudinales. Dans certaines circonstances, il peut être valable d’inclure la covariable « à effet aléatoire » (par exemple « centre ») comme covariable à effet fixe pendant l’étape d’imputation, puis d’utiliser une analyse par modèle mixte ou des équations d’estimation généralisées (EEG) pendant l’étape d’analyse. Cependant, l’application d’un modèle à effets mixtes (avec, par exemple, le « centre » comme effet aléatoire) implique que la structure multicouche des données doit être prise en considération lors de la modélisation de l’imputation multiple. Or, aucun logiciel commercial n’est directement disponible pour ce faire. Cependant, on peut utiliser le paquet REALCOME qui peut être interfacé avec STATA . L’interface exporte les données avec des valeurs manquantes de STATA vers REALCOM où l’imputation est effectuée en tenant compte de la nature multiniveau des données et en utilisant une méthode MCMC qui inclut des variables continues et qui, en utilisant un modèle normal latent, permet également un traitement correct des données discrètes. Les ensembles de données imputées peuvent ensuite être analysés à l’aide de la commande STATA ‘mi estimate:’ qui peut être combinée avec l’instruction ‘mixed’ (pour un résultat continu) ou l’instruction ‘meqrlogit’ pour un résultat binaire ou ordinal dans STATA. Dans l’analyse de données de panel, cependant, on peut facilement se trouver confronté à une situation où les données comprennent trois niveaux ou plus, par exemple, des mesures chez le même patient (niveau 1), des patients dans des centres (niveau 2), et des centres (niveau 3) . Pour ne pas s’engager dans un modèle assez compliqué qui peut conduire à un manque de convergence ou à des erreurs standard instables et pour lequel aucun logiciel commercial n’est disponible, nous recommandons soit de traiter l’effet centre comme fixe (directement ou suite à la fusion de petits centres en un ou plusieurs centres de taille appropriée, selon une procédure qui doit être prescrite dans le plan d’analyse statistique), soit d’exclure le centre comme covariable. Si la randomisation a été stratifiée par centre, cette dernière approche conduira à un biais vers le haut des erreurs standard résultant en une procédure de test quelque peu conservatrice .