Introduction aux statistiques commerciales

Considérez l’ensemble de données suivant .
4 ; 5 ; 6 ; 6 ; 7 ; 7 ; 7 ; 7 ; 7 ; 7 ; 8 ; 8 ; 8 ; 9 ; 10

Cet ensemble de données peut être représenté par l’histogramme suivant. Chaque intervalle a une largeur de un, et chaque valeur est située au milieu d’un intervalle.

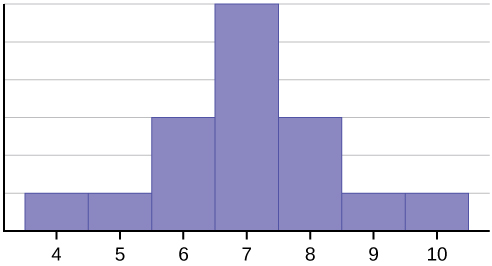
L’histogramme affiche une distribution symétrique des données. Une distribution est symétrique si une ligne verticale peut être tracée à un certain point de l’histogramme de sorte que la forme à gauche et à droite de la ligne verticale sont des images miroir l’une de l’autre. La moyenne, la médiane et le mode sont chacun sept pour ces données. Dans une distribution parfaitement symétrique, la moyenne et la médiane sont identiques. Cet exemple a un seul mode (unimodal), et le mode est le même que la moyenne et la médiane. Dans une distribution symétrique qui a deux modes (bimodale), les deux modes seraient différents de la moyenne et de la médiane.

L’histogramme pour les données : 4566677778 n’est pas symétrique. La partie droite semble « coupée » par rapport à la partie gauche. Une distribution de ce type est dite asymétrique à gauche car elle est tirée vers la gauche. Nous pouvons mesurer formellement l’asymétrie d’une distribution tout comme nous pouvons mesurer mathématiquement le poids central des données ou leur « spéciosité » générale. La formule mathématique de l’asymétrie est la suivante : . Plus l’écart par rapport à zéro est grand, plus l’asymétrie est importante. Si l’asymétrie est négative, la distribution est inclinée vers la gauche, comme dans la (Figure). Une mesure positive de l’asymétrie indique une asymétrie à droite comme dans (Figure).

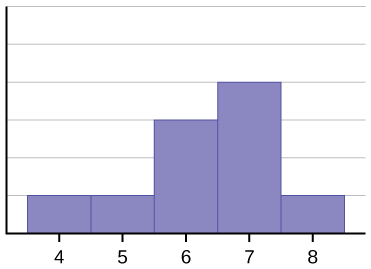
La moyenne est de 6,3, la médiane est de 6,5 et le mode est de sept. Remarquez que la moyenne est inférieure à la médiane, et qu’elles sont toutes deux inférieures au mode. La moyenne et la médiane reflètent toutes deux l’asymétrie, mais la moyenne la reflète davantage.

L’histogramme pour les données : 67777888910, n’est pas non plus symétrique. Il est incliné vers la droite.

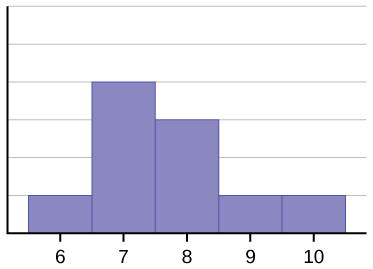
La moyenne est de 7,7, la médiane est de 7,5 et le mode est de sept. Des trois statistiques, la moyenne est la plus grande, tandis que le mode est le plus petit. Encore une fois, la moyenne reflète le plus l’asymétrie.

En résumé, généralement, si la distribution des données est asymétrique vers la gauche, la moyenne est inférieure à la médiane, qui est souvent inférieure au mode. Si la distribution des données est asymétrique vers la droite, le mode est souvent inférieur à la médiane, qui est inférieure à la moyenne.

Comme pour la moyenne, la médiane et le mode, et comme nous le verrons prochainement, la variance, il existe des formules mathématiques qui nous donnent des mesures précises de ces caractéristiques de la distribution des données. En regardant à nouveau la formule de l’asymétrie, nous voyons que c’est une relation entre la moyenne des données et les observations individuelles cubées.

où est l’écart type de l’échantillon des données, , et est la moyenne arithmétique et est la taille de l’échantillon.

Formellement, la moyenne arithmétique est connue comme le premier moment de la distribution. Le deuxième moment que nous allons voir est la variance, et l’asymétrie est le troisième moment. La variance mesure les différences au carré des données par rapport à la moyenne et l’asymétrie mesure les différences au cube des données par rapport à la moyenne. Alors que la variance ne peut jamais être un nombre négatif, la mesure de l’asymétrie peut l’être et c’est ainsi que nous déterminons si les données sont asymétriques à droite ou à gauche. L’asymétrie d’une distribution normale est de zéro, et toute donnée symétrique devrait avoir une asymétrie proche de zéro. Les valeurs négatives de l’asymétrie indiquent que les données sont inclinées vers la gauche et les valeurs positives de l’asymétrie indiquent que les données sont inclinées vers la droite. Par asymétrie à gauche, on entend que la queue de gauche est longue par rapport à la queue de droite. De même, l’asymétrie à droite signifie que la queue de droite est longue par rapport à la queue de gauche. L’asymétrie caractérise le degré d’asymétrie d’une distribution autour de sa moyenne. Alors que la moyenne et l’écart-type sont des quantités dimensionnelles (c’est pourquoi nous prendrons la racine carrée de la variance ) c’est-à-dire qu’elles ont les mêmes unités que les quantités mesurées , l’asymétrie est conventionnellement définie de manière à la rendre non dimensionnelle. C’est un nombre pur qui caractérise uniquement la forme de la distribution. Une valeur positive de l’asymétrie signifie une distribution dont la queue asymétrique s’étend vers un X plus positif et une valeur négative signifie une distribution dont la queue s’étend vers un X plus négatif. Une mesure nulle de l’asymétrie indiquera une distribution symétrique.

L’asymétrie et la symétrie deviennent importantes lorsque nous abordons les distributions de probabilité dans les chapitres suivants.

.