Comme pour le gâteau, vous pouvez avoir 2 petits morceaux ou 1 morceau deux fois plus gros et c’est la même quantité. D’où beaucoup de fractions sont équivalentes, comme 2/5 et 4/10.


Tout nombre peut être écrit comme une fraction
Ecrire tout nombre entier supérieur à 1 pour en faire une fraction puisque le nombre total de parties de tout entier indivis est un.
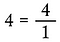
Multiplier des fractions en croix
Multiplier des fractions est facile, il suffit de multiplier en croix.
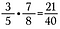
Note : les nombres mixtes doivent d’abord être transformés en fractions impropres, lisez la suite pour en savoir plus.
Multiplier par toute forme de un n’importe quand
Le nombre 1 est appelé l’identité multiplicative parce que nous pouvons le multiplier par n’importe quel nombre et le nombre reste le même. C’est important pour les fractions car souvent, nous devons modifier l’apparence d’une fraction sans changer réellement sa valeur.
Par exemple, je peux changer 1/3 en fraction équivalente 3/9 en multipliant par 3/3.
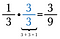
Ajouter et soustraire des parties de taille égale
Lorsqu’on ajoute et soustrait des fractions, les dénominateurs doivent être les mêmes. C’est logique. Si nous souhaitons combiner ou enlever des parties, nous devons parler de parties de même taille, sinon cela deviendrait confus.
Alors, que faites-vous si vos fractions n’ont pas les mêmes tailles ?
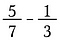
Multipliez par une forme de un pour changer les dénominateurs en une taille commune. En fait, nous divisons les fractions en plus petits morceaux jusqu’à ce qu’ils soient de la même taille. Cela s’appelle trouver un dénominateur commun.
En vérité, n’importe quel dénominateur commun fera l’affaire, mais les gens préfèrent trouver le plus petit. Dans ce cas, le plus petit nombre dans lequel à la fois 7 et 3 entrent sans reste est 21. Multipliez donc la première fraction par 3/3 et la seconde par 7/7.
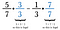
Si vous ne pouvez pas penser au plus petit dénominateur commun, vous pouvez toujours multiplier chaque fraction par la dénomination opposée. Parfois, comme dans ce cas, cela s’avère être le plus petit dénominateur commun. Si ce n’est pas le cas, réduisez simplement votre réponse à la fin.
Une fois que les dénominateurs correspondent, soustrayez les numérateurs pour obtenir 8/21.
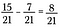
Cela fonctionne comme on peut s’y attendre. Pictorialement, commencez avec 15 pièces de 21 au total.

Retirez la coloration de 7 des 15 blocs bleus.

ce qui laisse 8/21 comme prévu.
Changer les nombres mixtes d’abord
Un nombre mixte est la combinaison d’un nombre entier et d’une fraction.
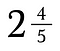
Les nombres mixtes ne jouent pas bien avec les autres fractions. C’est une bonne idée de les convertir d’abord en fractions impropres.
Note : Une fraction impropre est une fraction dont le numérateur est plus grand que son dénominateur donc ayant une valeur supérieure à un.
La conversion d’un nombre mixte est vraiment une addition
Pour convertir 2 et 4/5 en fraction impropre, ajoutez 2 + 4/5.
Étape 1 : Commencez par réécrire 2 comme 2/1.
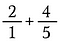
Étape 2 : Multiplier 2/1 par 5/5 pour obtenir une fraction équivalente de 10/5 dont le dénominateur commun souhaité est 5.
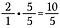
Étape 3 : additionner 10/5 + 4/5.
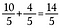
Notre résultat est la fraction impropre équivalente 14/5.
Pour reconvertir en nombre mixte, effectuez la division. Par exemple, 5 va dans 14 deux fois (puisque 5 x 2 = 10) avec 4 morceaux restants.
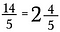
Comparer des fractions en utilisant le produit en croix
Supposons que nous voulions déterminer laquelle est la plus grande : 5/12 ou 6/13.
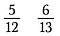
Première étape : Multiplier une diagonale et écrire le produit au-dessus du numérateur.
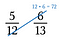
Deuxième étape : Multiplier l’autre diagonale et écrire son produit au-dessus de son numérateur.
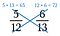
Troisième étape : Comparez les produits. Le côté avec le plus grand produit est la plus grande fraction. Donc, dans ce cas, 5/12 est inférieur à 6/13.
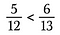
On peut aussi déterminer si les fractions sont égales en utilisant les produits en croix.
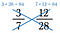
Le produit en croix de 3/7 et 12/28 sont tous les deux 84, donc 3/7 = 12/28.
Annulez tout ce qui se divise à un
La meilleure chose à propos des fractions est que vous pouvez trouver beaucoup d’occasions d’annuler. Ce qui les rend rapides et faciles à gérer.
Supposons que j’ai la fraction 8/10. On peut réécrire 8 et 10 avec 2 comme facteur.
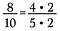
Parce que 2/2 = 1, je peux annuler les 2 en laissant 4/5 comme fraction réduite.
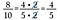
Utilisez cette stratégie pour faciliter également la multiplication des fractions.
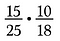
Commencez par réécrire chaque nombre en facteurs.
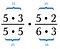
Annulez toutes les paires de nombres qui se divisent à 1. Par exemple, 5/5 = 1.
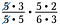
J’ai une autre paire de 5 ainsi qu’une paire de 3 qui se divisent en 1 également.
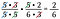
Oops ! J’aurais pu réécrire 6 comme 2 x 3 et annuler une paire de 2. Ce n’est pas grave si vous manquez un facteur, continuez jusqu’à ce que vous les ayez tous.
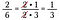
Si j’avais multiplié 15/25 fois 10/18 directement cela aurait été beaucoup d’arithmétique, en utilisant l’annulation je pré-réduis les fractions et rend la multiplication plus simple.
Utiliser la multiplication pour diviser des fractions
Le concept de division des fractions est facile avec des exemples simples comme:

Il y a deux moitiés dans un tout, donc il y a 10 moitiés dans 5 tout.
Mais le concept devient délicat avec des fractions plus compliquées.
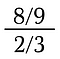
Pour résoudre ce problème, nous utiliserons deux faits:
- Nous pouvons multiplier par toute forme de un (i.e n’importe quoi sur lui-même)
- Multiplier par l’inverse de 3/2, qui est 2/3, donne 1 par annulation
Première étape : Commencer par multiplier par la réciproque sur elle-même.
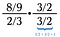
Maintenant nous avons deux plus petits problèmes à résoudre (bleu et vert).
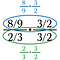
Deuxième étape : Annulez tout ce qui divise à 1 dans la fraction inférieure (verte). Cela devrait toujours donner 1.

Il nous reste maintenant le problème du haut à résoudre.
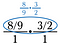
Troisième étape : Utilisez l’annulation pour pré-réduire la fraction. Après avoir effectué ces réductions, multipliez en croix pour obtenir 4/3.

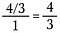
Shortcut
C’est la mécanique de la main longue de « retourner et multiplier ». »
Nous pouvons sauter la multiplication par la réciproque en bas puisqu’elle s’annule toujours à 1. Par conséquent, tout ce que vous devez faire est de multiplier le numérateur par la réciproque du dénominateur.

Bonus : Théorie, au cas où vous seriez intéressé…
Grande question ! Pour généraliser, faites deux fractions en utilisant les lettres a, b, c et d pour représenter quatre nombres différents.
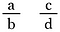
Multipliez les deux fractions par b-d (cela nous permettra d’annuler les dénominateurs).
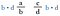
On annule maintenant les b de gauche et les d de droite puisqu’ils se divisent à 1. Nous n’avons plus de fractions, juste les produits d-a et c-b.
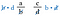
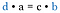
Regardez les fractions initiales. Ce sont les mêmes produits que si nous avions multiplié les diagonales. Par conséquent, le raccourci est de comparer le produit en croix.
❤ STAY CONNECTED ❤
Rester à jour avec tout ce que Math Hacks fait!