Les équations de Lotka-Volterra décrivent un modèle écologique prédateur-proie (ou parasite-hôte) qui suppose que, pour un ensemble de constantes positives fixes 
(le taux de croissance des proies), 
(le taux auquel les prédateurs détruisent les proies), 
(le taux de mortalité des prédateurs), et 
(le taux auquel les prédateurs augmentent en consommant les proies), les conditions suivantes sont réunies.
1. Une population de proies 
augmente à un taux 
(proportionnel au nombre de proies) mais est simultanément détruite par les prédateurs à un taux 
(proportionnel au produit du nombre de proies et de prédateurs).
2. Une population de prédateurs 
diminue à un taux 
(proportionnel au nombre de prédateurs), mais augmente à un taux 
(à nouveau proportionnel au produit du nombre de proies et de prédateurs).
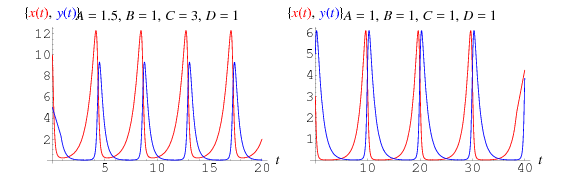
Cela donne les équations différentielles couplées
 |
 |
 |
(1)
|
 |
 |
 |
(2)
|
dont les solutions sont tracées ci-dessus, où les proies sont représentées en rouge, et les prédateurs en bleu. Dans ce genre de modèle, la courbe des proies mène toujours à celle des prédateurs.
Les points critiques se produisent lorsque 
, alors
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
Le seul point stationnaire est donc situé en 
.