En géométrie, il existe plusieurs types de quadrilatère à savoir le parallélogramme, le losange, le carré, le rectangle, le trapèze et le cerf-volant, qui partagent des caractéristiques communes, en raison desquelles les gens rencontrent des difficultés à comprendre ces figures. Le losange est un carré oblique dont les côtés adjacents sont égaux. Au contraire, un parallélogramme est un rectangle oblique avec deux ensembles de côtés opposés parallèles.
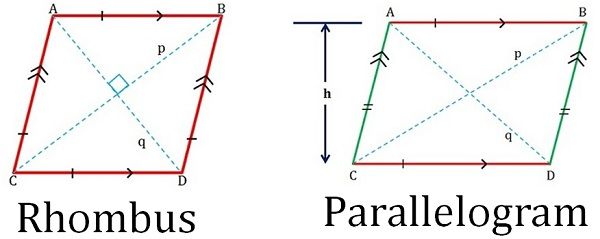
La différence fondamentale entre le losange et le parallélogramme réside dans leurs propriétés, c’est-à-dire que tous les côtés d’un losange ont la même longueur, alors que le parallélogramme est une figure rectiligne dont les côtés opposés sont parallèles.
Contenu : Rhombus Vs Parallélogramme
- Tableau de comparaison
- Définition
- Différences clés
- Conclusion
Tableau de comparaison
.
| Base de comparaison | Rhombus | Parallélogramme |
|---|---|---|
| Message | Rhombus fait référence à une figure plate, une figure à quatre côtés dont tous les côtés sont congruents. | Un parallélogramme est une figure plate à quatre côtés, dont les côtés opposés sont parallèles entre eux. |
| Côtés égaux | Les quatre côtés ont la même longueur. | Les côtés opposés ont la même longueur. |
| Diagonales | Les diagonales se coupent à angle droit en formant un triangle scalène. | Les diagonales se coupent en formant deux triangles congruents. |
| Aire | (pq)/2, où p et q sont les diagonales | bh, où b = base et h = hauteur |
| Périmètre | 4 a, où a = côté | 2 (a+b), où a = côté, b = base |
Définition du losange
Un quadrilatère dont la longueur des côtés est congrue est appelé losange. Il est de forme plate et a quatre côtés ; dans lequel les côtés en vis-à-vis sont parallèles les uns aux autres (voir figure donnée ci-dessous).
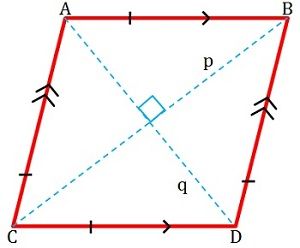Les angles opposés d’un losange sont égaux c’est-à-dire de même degré. Ses diagonales se rencontrent à 90 degrés (angle droit), donc perpendiculaires entre elles et forment deux triangles équilatéraux. Ses côtés adjacents sont supplémentaires, ce qui signifie que la somme de leur mesure est égale à 180 degrés. Il est également connu sous le nom de parallélogramme équilatéral.
Définition du parallélogramme
Un parallélogramme comme son nom l’indique est est décrit comme une figure de forme plate, ayant quatre côtés dont l’ensemble des côtés opposés sont parallèles et congruents (voir figure donnée ci-dessous).
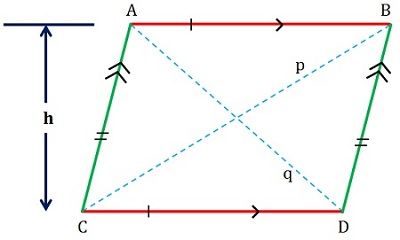La mesure de ses angles opposés est égale et les angles consécutifs sont supplémentaires, c’est-à-dire que la somme de leur mesure est égale à 180 degrés. Ses diagonales se coupent en deux qui forment deux triangles congruents.
Différences clés entre le losange et le parallélogramme
La différence entre le losange et le parallélogramme peut être dessinée clairement sur les bases suivantes:
- Nous définissons le losange comme un quadrilatère à quatre côtés de forme plate dont la longueur de tous les côtés est congrue. Un parallélogramme est une figure plate à quatre côtés, dont les côtés opposés sont parallèles entre eux.
- Tous les côtés du losange sont de même longueur alors que seuls les côtés opposés d’un parallélogramme sont égaux.
- Les diagonales d’un losange se coupent en deux à angle droit formant deux triangles scalènes. Par opposition à un parallélogramme dont les diagonales se coupent en deux formant deux triangles congruents.
- La formule mathématique de l’aire du losange est (pq)/2, où p et q sont les diagonales. A l’inverse, l’aire du parallélogramme peut être calculée en multipliant la base et la hauteur.
- Le périmètre du losange peut être calculé à l’aide de la formule suivante – 4 a, où a = côté du losange. Au contraire, le périmètre du parallélogramme peut être calculé en – additionnant la base et la hauteur, et en multipliant la somme par 2.
Conclusion
Le parallélogramme et le losange sont tous deux des quadrilatères, dont les côtés en vis-à-vis sont parallèles, les angles opposés sont égaux, la somme des angles intérieurs est de 360 degrés. Un losange est lui-même un type particulier de parallélogramme. Par conséquent, on peut dire que tout losange est un parallélogramme, mais l’inverse n’est pas possible.
.