Concave vs convexe?

Quelle est la différence entre concave et convexe?

Si nous devions décrire la différence entre concave et convexe de la manière la plus générale possible, nous dirions que tout objet creux, ressemblant à un bol, est concave, tandis que tout objet ressemblant à un ballon de rugby ou de football a une forme convexe. Mais peut-être que la raison pour laquelle convexe et concave sont si souvent mal utilisés est que ces deux mots ne sont pas aussi simples que nous le souhaiterions.

La plupart des sources grammaticales insistent sur la façon dont l’utilisation de moyens mnémotechniques est possible pour déchiffrer convexe et concave à travers le mot caverne. Alors que la notion d’associer concave avec l’événement de quelque chose « caver » aide à apprendre sur les caractéristiques de surface, il est confus de relier cette idée vers des sujets impliquant des graphiques.

Pour comprendre comment concave et convexe sont différents les uns des autres, nous devons apprendre comment chaque terme est utilisé dans la capacité des mathématiques, des miroirs, des lentilles, et, enfin, au sein de l’écriture créative. Une fois que vous avez décidé du contexte dans lequel vous souhaitez utiliser des mots comme concave et convexe, l’apprentissage de leurs aspects techniques vous permettra d’être plus confiant quant à leur utilisation dans le langage courant.

Que signifie concave ?

Concave est utilisé comme adjectif ou nom pour décrire la forme d’un objet ou d’une surface qui est courbée vers l’intérieur ou creusée comme un bol. Voici quelques exemples de concave dans une phrase,

« Elle a écopé la crème glacée du récipient, laissant une empreinte concave. »

Selon le Oxford Dictionary of Word Histories, le mot concave provient du moyen anglais tardif. Concave et concavité rendent le terme latin concavus (con- et cavus), qui se traduit par  » ensemble  » et  » creux  » ( » Concave « , 110).

Les synonymes de concave comprennent :

Denté, déprimé, bombé, creux, échancré, en retrait et enfoncé.

Les antonymes de concave comprennent :

Bulleux, cambré, saillant, proéminent, protubérant.

Que signifie convexe ?

Le mot convexe, ou convexité, est un adjectif décrivant un objet ou une surface arrondie ou incurvée. En ce qui concerne les objets, la surface médiane d’un objet convexe est plus large que son coin extérieur. Voici quelques exemples de convexe dans une phrase,

« Je suis tombé dans du sumac vénéneux et j’ai maintenant des bosses rouges et convexes sur toute ma peau. »

Les synonymes de convexe comprennent :

Arché, courbé, bombé, relevé.

Les antonymes de convexe comprennent :

Encombrement, enfoncement.

Fonctions concaves vs convexes

Une fonction convexe représente une ligne continue sur un graphique où le point médian, ou entier médian d’un domaine, ne dépasse pas la moyenne de l’intervalle. Une fonction concave est l’exact opposé d’une fonction convexe car, pour que f(x) soit concave, f(x) doit être négative. Pour rendre les différences plus claires, voici un rapide aperçu de la façon dont les termes se comparent :

Concave vers le haut = convexe = convexe vers le bas

Concave vers le bas = concave = convexe vers le haut

La différence entre les fonctions concave et convexe apparaît plus clairement si nous regardons un graphique. Remarquez comment la fonction convexe s’ouvre vers le haut, tandis que la fonction concave s’ouvre vers le bas.

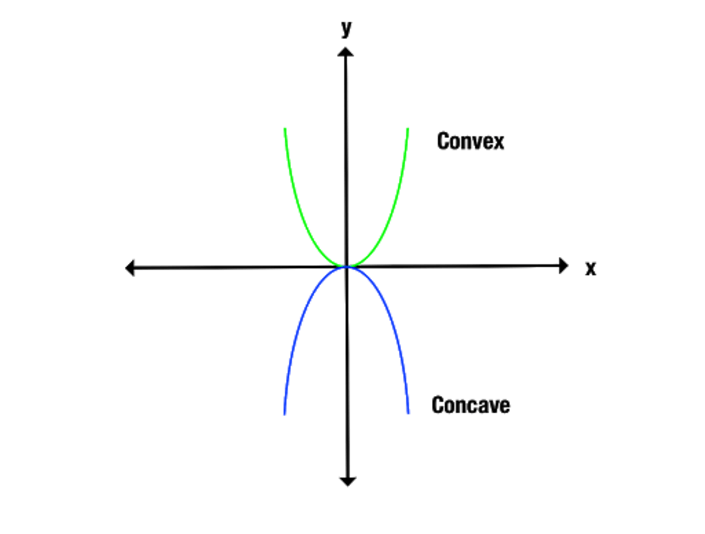
Une autre façon d’identifier les fonctions concaves et convexes est de relier les points du graphique le long de l’axe des x. Une fonction concave ne relie que des lignes en dessous du graphique, tandis qu’une fonction convexe ne produit que des lignes au-dessus du graphique.

Nous pouvons en outre utiliser le calcul pour déchiffrer si une fonction est convexe ou concave ou non. Si la dérivée seconde de f(x) est supérieure à zéro, alors la fonction est convexe. Mais si la dérivée seconde de f(x) est inférieure à zéro, la fonction est concave.

Polygones convexes vs concaves

Pas de panique, mais les mots convexe et concave sont aussi utilisés pour la géométrie aussi. Les formes convexes et concaves sont le plus souvent abordées en référence aux polygones, qui sont des formes avec un minimum de trois côtés et angles.

Les polygones réguliers existent avec des côtés et des angles égaux, mais les polygones convexes et concaves sont un peu plus compliqués. Les polygones convexes contiennent des angles intérieurs qui sont inférieurs à 180 degrés, tandis que les polygones concaves contiennent un ou plusieurs angles intérieurs supérieurs à 180 degrés.

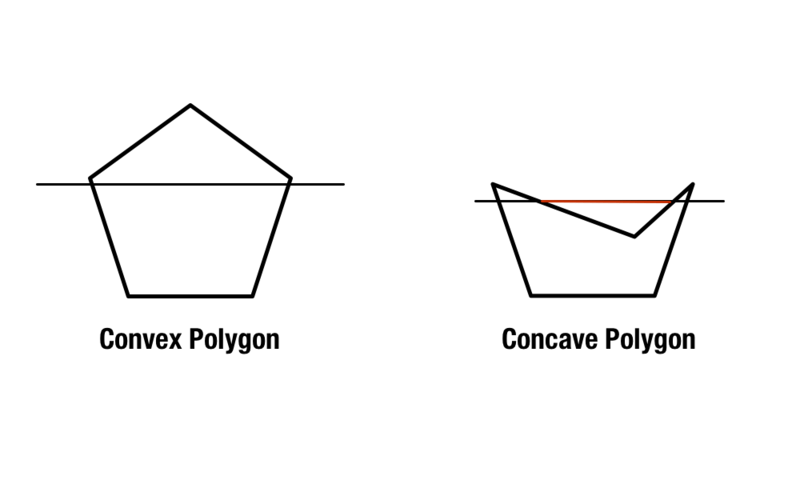
Une deuxième méthode pour identifier les polygones concaves et convexes consiste à tracer deux lignes diagonales à travers la forme, en partant des coins de la forme. Si chaque ligne existe à l’intérieur de la forme, la forme est convexe. S’il y a au moins une ligne qui traverse à l’extérieur de la forme, elle est concave.

Miroirs concaves vs convexes

Les mots concave et convexe sont couramment utilisés lorsqu’on parle d’objets optiques, comme les miroirs et les lentilles. Toute surface convexe fera saillie vers l’extérieur, comme une bulle, ce qui donne un effet de largeur. Les miroirs convexes sont couramment trouvés à l’intérieur des garages de stationnement, où les conducteurs ont besoin d’une vue large autour des coins ou des angles morts potentiels.

A l’inverse, un miroir concave est incurvé vers l’intérieur et produit un reflet agrandi à l’envers. Comme l’a montré l’école de physique de l’université du Pays de Galles du Sud, toute personne possédant une cuillère brillante peut tester cette observation en regardant son reflet dans la cuillère. Sur la surface concave de la cuillère, là où vous prenez votre nourriture, votre reflet est déformé de manière étroite, et vous apparaissez à l’envers. Mais si vous retournez votre cuillère sur le côté convexe, votre reflet sera droit et plus petit.

Les reflets varient tellement entre les surfaces convexes et concaves parce que, que la surface soit ou non courbée vers l’extérieur ou vers l’intérieur, le miroir lui-même fait partie d’une sphère. Comme la surface d’une sphère n’est pas plate, la lumière réfléchie par sa surface parcourra des distances différentes avant d’entrer en contact avec le miroir.

Selon la zone de la surface avec laquelle la lumière entre en contact, un rayon de lumière peut se réfléchir sur des surfaces voisines pour produire une zone de visibilité plus focalisée. C’est pourquoi, en regardant la surface intérieure d’une cuillère, on pourrait ne voir que le reflet de ce qui est le plus proche de la surface de la cuillère… même si elle semble toujours plus petite. En outre, si vous deviez placer votre doigt à l’intérieur de la cuillère, la surface du miroir peut produire deux ou trois reflets différents en même temps.

Lentille concave contre lentille convexe

Les lentilles concaves et convexes existent dans les objets de tous les jours comme les lunettes, les lentilles, les jumelles et les télescopes. De même que la science derrière la réflexion de la lumière sur les miroirs convexes et concaves, il existe également des modèles pour la façon dont la lumière passe à travers les lentilles concaves et convexes pour produire une image visible.

Lentilles convexes

Selon l’Académie Manocha, les lentilles convexes sont appelées lentilles convergentes en raison de leur capacité à produire des images diminuées, agrandies ou introverties. La précision avec laquelle une image apparaît à travers la lentille convexe dépend de la proximité de l’objet par rapport au point focal de la lentille. Pour toute lentille convexe, il existe des points focaux symétriques de chaque côté de la lentille.

La précision avec laquelle un objet est produit à travers une lentille convexe est prédite par trois principes :

Principe 1 : Tout rayon lumineux qui traverse une lentille convexe est parallèle à l’axe principal, qui est une ligne centrale passant par le centre absolu d’une lentille sphérique. Une fois que la lumière entre en contact avec la lentille, elle se réfracte et passe par le point focal de l’autre côté. Les rayons lumineux passants qui sont parallèles à l’axe principal voyagent au-dessus de l’objet devant la lentille.

Principe 2 : Tout rayon lumineux qui passe par le centre d’une lentille convexe continuera en ligne droite de l’autre côté.
Principe 3 : Tout rayon de lumière qui est passé par un point focal du même côté que l’objet se réfractera au contact de la lentille et deviendra parallèle à l’axe principal de l’autre côté.

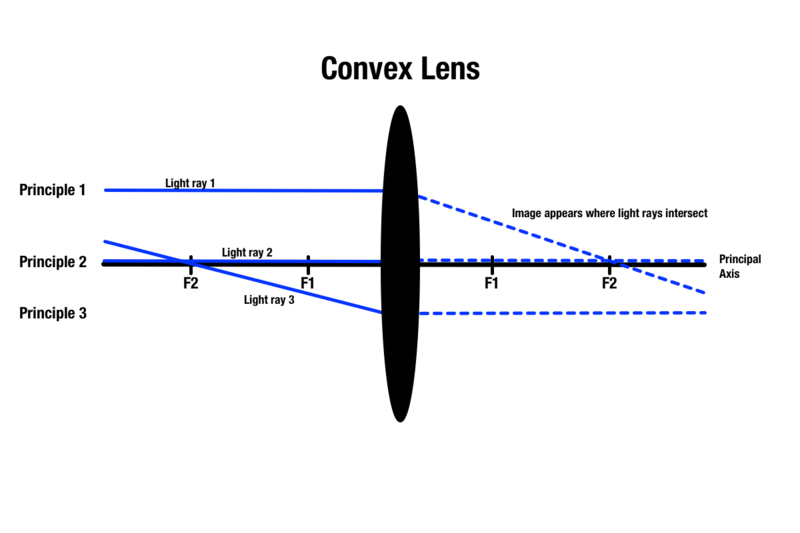
Bien qu’il existe trois principes pour prédire la qualité de l’image à travers une lentille convexe, seuls deux principes peuvent s’appliquer à un objet lors du dessin d’un diagramme de rayons. N’importe quels deux principes produiront une intersection de lumière de l’autre côté de la lentille, qui indiquera la zone où l’image de l’objet apparaît.

Plus un objet est éloigné d’une lentille convexe, plus l’image sera petite de l’autre côté, et plus un objet est proche de la lentille convexe, plus il apparaîtra grand. Un objet situé au-delà du point focal le plus proche produit une image plus grande derrière l’objet. Comme le souligne l’Académie Manocha, ce type de grossissement de lentille est utilisé pour les outils optiques tels que les loupes.

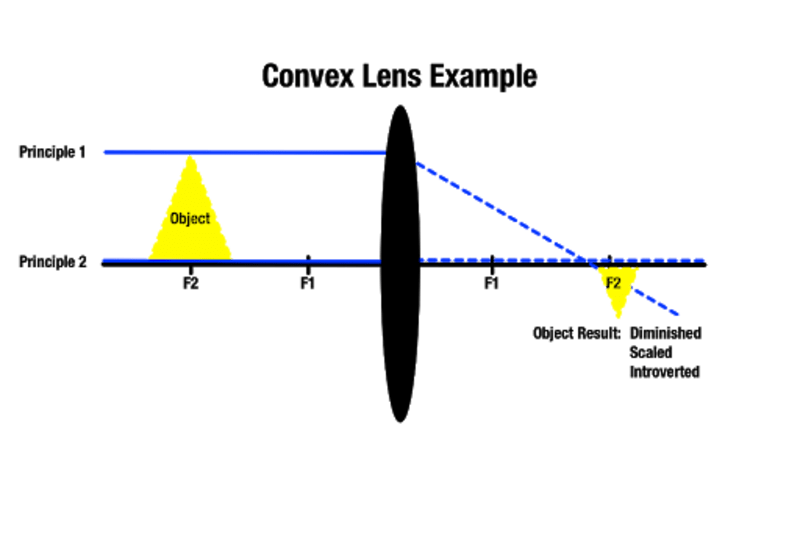
Selon le point focal où se trouve un objet, il est possible de produire une image dont la taille est approximative. Il est également possible de créer des images réelles qui ne sont pas visibles si les rayons lumineux qui passent ne se croisent jamais parce qu’ils sont parallèles de l’autre côté. Dans ce cas, l’image produite existe à une distance infinie.

Lentilles concaves

Toute lentille concave aura un diamètre plus épais, et un centre plus mince puisqu’une lentille concave est courbée vers l’intérieur. La forme des lentilles concaves permet à la lumière de s’étaler une fois qu’elle entre en contact avec la lentille, ce qui permet aux objets virtuels d’apparaître plus petits. La capacité de la lentille concave à étaler la lumière en fait une lentille idéale pour des outils tels que les lampes de poche, où une source centrale de lumière peut être utilisée sur une plus grande surface.

Les lentilles concaves produisent des images avec trois principes qui sont similaires aux lentilles convexes :

Principe 1 : Tout rayon de lumière voyageant au-dessus de l’objet et parallèle à l’axe principal se réfractera au contact de la lentille et apparaîtra comme s’il provenait de la direction du point focal le plus proche.

Principe 2 : Tout rayon lumineux passant par le centre de la lentille concave la traversera sans réfraction.
Principe 3 : Tout rayon lumineux dirigé vers un point focal situé de l’autre côté de la lentille concave se réfractera et deviendra parallèle à l’axe principal.

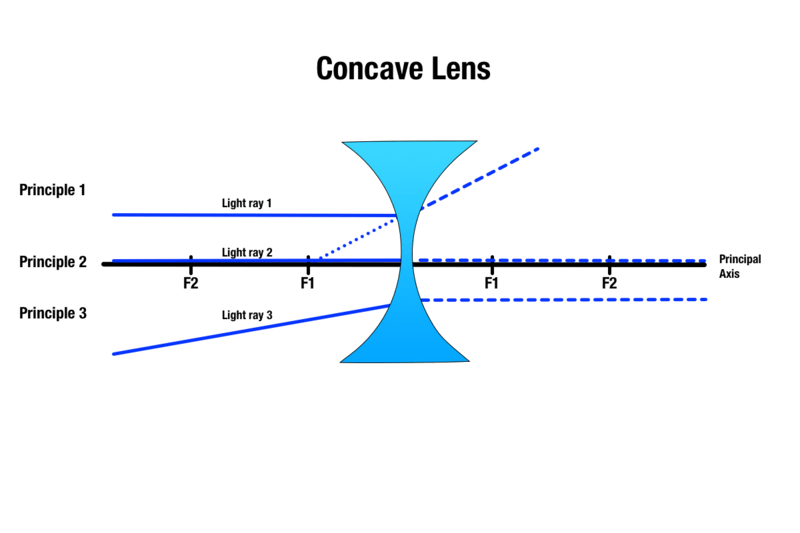
Bien que la taille de l’image de l’objet varie en fonction de la distance de l’objet à une lentille concave, l’image produite est toujours virtuelle, verticale, plus petite, et apparaît du même côté de la lentille que l’objet.

Concave vs convexe à l’écrit

Les mots concave et convexe sont opposés l’un à l’autre, et ils décrivent essentiellement la forme des objets ou des surfaces de la même manière que nous opposons des mots comme :

• petit vs. big
• Tall vs. short
• Slim vs. wide
• Round vs. flat

Parce que concave et convexe sont des mots techniques, les utiliser de manière descriptive pour la prose peut produire une interprétation plus métaphorique ou abstraite pour les audiences occasionnelles. Ce que cela signifie, c’est que si les écrivains décident d’utiliser concave ou convexe en dehors du domaine de leur utilisation typique, l’écrivain doit décider à quel point il veut que son écriture soit claire.

Considérer l’adjectif

Un exemple proéminent de l’utilisation concave ou convexe en littérature est de considérer les écrits de l’auteur américain David Foster Wallace (ou DFW pour faire court). DFW est connu pour son style d’écriture complexe et technique – et oui, il a utilisé convexe et concave pour décrire des noms à plusieurs reprises. Wallace utilise concave et convexe dans les exemples suivants :

« Mon œil de main était correct, mais je n’étais ni grand ni rapide, j’avais une poitrine presque concave et des poignets si minces que je pouvais les braquer avec un pouce et un auriculaire… »

– « Tennis, Trigonométrie, Tornades : A Midwestern Boyhood », Harper’s Magazine.

« …des yeux de poupée qui s’ouvrent avec la traction d’une corde de coeur, concave où je suis convexe. »

– « Ordre et flux à Northampton, » Conjonctions.

Le but de l’utilisation des exemples DFW n’est pas simplement de montrer comment les écrivains ont utilisé convexe ou concave en dehors du contexte mathématique, mais plutôt, pour les écrivains, de se demander si l’utilisation de termes techniques ou abstraits est utile pour communiquer clairement à leur public.
Dans le premier exemple de DFW, l’utilisation de concave est logique car il décrit la structure de quelque chose. Mais, l’utilisation de concave et convexe pour décrire des noms non objectifs, tels que des sentiments ou des pensées, a tendance à obscurcir le sens de ce que nous essayons d’expliquer. Le deuxième exemple DFW marche sur une ligne fine tout en utilisant convexe et concave parce que leur utilisation est à la fois littérale et métaphorique.

FAQ : Termes connexes

Qu’est-ce qu’une fonction ?

Une fonction est l’équation d’une ligne sur un graphique. Les fonctions sont différentes pour chaque ligne sur un graphique, mais elles prennent la forme générale de,

f(x) = x + 1

Avec toute fonction linéaire, la variable dépendante est généralement f(x), tandis que toute variable inconnue dans la fonction est appelée variable indépendante.

Qu’est-ce que le domaine ?

Le domaine est un ensemble de variables indépendantes sur un graphique qui correspond à la fonction d’une ligne. Les domaines sont importants à comprendre car ils localisent des points spécifiques sur le graphique qui correspond à toute sortie réelle d’une équation.

Qu’est-ce que l’étendue ?

L’étendue de toute fonction représente toute valeur possible le long de l’axe des x ou des y sur un graphique qui produit une valeur valide pour la variable dépendante. Tous les nombres entiers minimum et maximum sont identifiés en substituant des variables à l’axe des x ou des y.

Qu’est-ce qu’un intervalle ?

Un intervalle est un ensemble de nombres qui représentent les entiers d’une ligne, alias le domaine. Un intervalle fermé comprend deux points finis d’une ligne, où la ligne n’existe plus en dehors du domaine d’un nombre entier. Un intervalle ouvert est un ensemble d’entiers qui ne représentent pas l’extrémité absolue du domaine d’une ligne.

Testez vous!

Voyez si vous comprenez bien la différence entre convexe et concave avec les questions à choix multiples suivantes:

1. En regardant une cuillère brillante, vous remarquez que votre reflet est à l’envers. La surface de la cuillère est une surface _________.
   a. Convexe
   b. Miroir
   c. Concave
   d. Métal
2. En termes de représentation graphique des fonctions, une fonction convexe est parfois appelée :
   a. Concave vers le haut
   b. Convexe vers le bas
   c. Concave vers le bas
   d. A et B
3. Laquelle des propositions suivantes ne décrit pas une surface concave :
   a. Demi-sphère creuse
   b. Lentille oculaire
   c. Bol de céréales
   d. Hémisphère
4. Lequel des éléments suivants ne décrit pas une surface convexe :
   a. Le personnage Stewie de Family Guy
   b. Sphère
   c. Miroir de garage de stationnement
   d. Football
5. Laquelle des formes suivantes ne peut pas exister en tant que polygone concave :
   a. Pentagone
   b. Hexagone
   c. Triangle
   d. Octogone

Réponses

1. C : Concave
2. D : A et B
3. D : Hémisphère
4. B : Sphère
5. C : Triangle

Sources:

1. Bourne, M. « Domaine et étendue d’une fonction ». Mathématiques interactives, 4 janvier 2019.
2. « Concave ». Dictionnaire Merriam-Webster, 2019.
3. « Concave. » The Oxford Dictionary of Word Histories, Ed. Chantrell, 2002, p. 110.
4. « Miroirs concaves et convexes ». Académie Manocha, YouTube, 2019.
5. « Lentille concave : Définition & Utilisations. » Study.com, 2019.
6. « Convexe ». Dictionnaire Merriam-Webster, 2019.
7. « Lentilles convexes et concaves ». Académie Manocha, YouTube, 2019.
8. « Mathématiques / Comprendre les polygones ». Learnhive Inc, 2018.
9. « Réflexion sur un miroir concave ». UNSW Physics, YouTube, 2017.
10. Wallace, D.F. « Tennis, trigonométrie, tornades : A Midwestern Boyhood. » Harper’s Magazine, 1991.
11. Wallace, D.F. « Ordre et flux à Northampton ». Conjonctions, 1991.
12. Weisstein, Eric W. « Fonction concave ». MathWorld-A Wolfram Web Resource, s.d.
13. Weisstein, Eric W. « Fonction convexe. » MathWorld-A Wolfram Web Resource, n.d.

Le compteur de mots est un outil dynamique en ligne utilisé pour compter les mots, les caractères, les phrases, les paragraphes et les pages en temps réel, ainsi que pour vérifier l’orthographe et la grammaire.