Récemment, un de mes collègues m’a posé quelques questions comme » pourquoi avons-nous autant de fonctions d’activation ? », « pourquoi celle-là fonctionne mieux que l’autre ? », « comment savoir laquelle utiliser ? », « est-ce que ce sont des maths hardcore ? » et ainsi de suite. J’ai donc pensé, pourquoi ne pas écrire un article à ce sujet pour ceux qui sont familiers avec le réseau neuronal seulement à un niveau de base et est donc, se demandant sur les fonctions d’activation et leur « pourquoi-comment-mathématiques ! ».
NOTE : Cet article suppose que vous avez une connaissance de base d’un « neurone » artificiel. Je vous recommande de vous documenter sur les bases des réseaux neuronaux avant de lire cet article pour une meilleure compréhension.
Fonctions d’activation
Alors, que fait un neurone artificiel ? En termes simples, il calcule une « somme pondérée » de son entrée, ajoute un biais et décide ensuite s’il doit être « tiré » ou non ( oui c’est vrai, c’est une fonction d’activation qui fait cela, mais suivons le mouvement pour un moment ).
Donc, considérons un neurone.
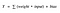
Maintenant, la valeur de Y peut être n’importe quoi allant de -inf à +inf. Le neurone ne connaît pas vraiment les limites de cette valeur. Alors, comment décider si le neurone doit se déclencher ou non (pourquoi ce schéma de déclenchement ?) ? Parce que nous l’avons appris de la biologie c’est la façon dont fonctionne le cerveau et le cerveau est un témoignage de travail d’un système génial et intelligent ).
Nous avons décidé d’ajouter des « fonctions d’activation » à cette fin. Pour vérifier la valeur Y produite par un neurone et décider si les connexions extérieures doivent considérer ce neurone comme « tiré » ou non. Ou plutôt disons – « activé » ou non.
Fonction d’activation
La première chose qui nous vient à l’esprit est pourquoi pas une fonction d’activation basée sur un seuil ? Si la valeur de Y est supérieure à une certaine valeur, déclarez-la activée. Si elle est inférieure au seuil, on dit qu’elle ne l’est pas. Hmm super. Cela pourrait fonctionner !
Fonction d’activation A = « activée » si Y > seuil sinon non
Alternativement, A = 1 si y> seuil, 0 sinon
Bien, ce que nous venons de faire est une « fonction à pas », voir la figure ci-dessous.
Sa sortie est 1 ( activée) quand la valeur > 0 (seuil) et sort un 0 ( non activé) sinon.
Génial. Cela fait donc une fonction d’activation pour un neurone. Pas de confusions. Cependant, il y a certains inconvénients avec cela. Pour mieux le comprendre, pensez à ce qui suit.
Supposons que vous créez un classificateur binaire. Quelque chose qui devrait dire un « oui » ou un « non » ( activer ou ne pas activer ). Une fonction Step pourrait le faire pour vous ! C’est exactement ce qu’elle fait, dire un 1 ou un 0. Maintenant, pensez au cas d’utilisation où vous voudriez que plusieurs neurones de ce type soient connectés pour faire apparaître plus de classes. Classe 1, classe 2, classe 3, etc. Que se passera-t-il si plus d’un neurone est « activé ». Tous les neurones produiront un 1 (à partir de la fonction d’étape). Maintenant, que décideriez-vous ? Quelle est la classe ? Hmm difficile, compliqué.
Vous voudriez que le réseau n’active qu’un seul neurone et que les autres soient à 0 ( seulement alors vous pourriez dire qu’il a classé correctement/identifié la classe ). Ah ! C’est plus difficile à entraîner et à converger de cette façon. Il aurait été préférable que l’activation ne soit pas binaire et que l’on dise plutôt « 50% activé » ou « 20% activé » et ainsi de suite. Et puis si plus d’un neurone s’active, on pourrait trouver quel neurone a la « plus haute activation » et ainsi de suite ( mieux que max, un softmax, mais laissons cela pour l’instant ).
Dans ce cas aussi, si plus d’un neurone dit « 100% activé », le problème persiste.Je sais ! Mais..puisqu’il y a des valeurs d’activation intermédiaires pour la sortie, l’apprentissage peut être plus lisse et plus facile ( moins ondulatoire ) et les chances que plus d’un neurone soit activé à 100% sont moindres par rapport à la fonction d’étape pendant la formation ( cela dépend aussi de ce que vous formez et des données ).
Ok, donc nous voulons quelque chose qui nous donne des valeurs d’activation intermédiaires ( analogiques ) plutôt que de dire « activé » ou non ( binaire ).
La première chose qui nous vient à l’esprit serait la fonction linéaire.
Fonction linéaire
A = cx
Une fonction linéaire où l’activation est proportionnelle à l’entrée ( qui est la somme pondérée du neurone ).
De cette façon, elle donne une gamme d’activations, donc ce n’est pas une activation binaire. Nous pouvons certainement connecter quelques neurones ensemble et si plus d’un feu, nous pourrions prendre le maximum ( ou softmax) et décider en fonction de cela. C’est donc également possible. Alors quel est le problème avec ceci ?
Si vous êtes familier avec la descente de gradient pour la formation, vous remarquerez que pour cette fonction, la dérivée est une constante.
A = cx, la dérivée par rapport à x est c. Cela signifie que le gradient n’a aucune relation avec X. C’est un gradient constant et la descente va être sur le gradient constant. S’il y a une erreur de prédiction, les modifications apportées par la rétropropagation est constante et ne dépend pas de la modification de l’entrée delta(x) !!!
Ce n’est pas si bon que cela ! ( pas toujours, mais soyez indulgent avec moi ). Il y a aussi un autre problème. Pensez aux couches connectées. Chaque couche est activée par une fonction linéaire. Cette activation va à son tour dans le niveau suivant comme entrée et la deuxième couche calcule la somme pondérée sur cette entrée et elle se déclenche à son tour sur la base d’une autre fonction d’activation linéaire.
Qu’importe le nombre de couches que nous avons, si toutes sont linéaires par nature, la fonction d’activation finale de la dernière couche n’est rien d’autre qu’une simple fonction linéaire de l’entrée de la première couche ! Faites une pause et pensez-y.
Cela signifie que ces deux couches ( ou N couches ) peuvent être remplacées par une seule couche. Ah ! Nous venons de perdre la capacité d’empiler des couches de cette façon. Peu importe comment nous empilons, le réseau entier est toujours équivalent à une seule couche avec une activation linéaire ( une combinaison de fonctions linéaires de manière linéaire est toujours une autre fonction linéaire ).
Passons à autre chose, n’est-ce pas ?
Fonction Sigmoïde
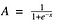
Bien, cela semble lisse et « step function like ». Quels en sont les avantages ? Réfléchissez-y un instant. Tout d’abord, elle est non linéaire par nature. Les combinaisons de cette fonction sont également non linéaires ! Super. Maintenant on peut empiler des couches. Et les activations non binaires ? Oui, ça aussi ! Cela donnera une activation analogique contrairement à la fonction de pas. Elle a un gradient lisse aussi.
Et si vous remarquez, entre les valeurs de X -2 à 2, les valeurs de Y sont très raides. Ce qui signifie que tout petit changement dans les valeurs de X dans cette région entraînera un changement significatif des valeurs de Y. Ah, cela signifie que cette fonction a tendance à amener les valeurs de Y aux deux extrémités de la courbe.
On dirait qu’elle est bonne pour un classificateur compte tenu de sa propriété ? Oui ! elle l’est en effet. Il a tendance à amener les activations de part et d’autre de la courbe ( au-dessus de x = 2 et en dessous de x = -2 par exemple). Faire des distinctions claires sur la prédiction.
Un autre avantage de cette fonction d’activation est que, contrairement à la fonction linéaire, la sortie de la fonction d’activation va toujours être dans la plage (0,1) par rapport à (-inf, inf) de la fonction linéaire. Ainsi, nos activations sont liées à un intervalle. Bien, ça ne fera pas exploser les activations alors.
C’est génial. Les fonctions sigmoïdes sont l’une des fonctions d’activation les plus utilisées aujourd’hui. Alors quels sont les problèmes que cela pose ?
Si vous remarquez, vers chaque extrémité de la fonction sigmoïde, les valeurs Y ont tendance à répondre très peu aux changements de X. Qu’est-ce que cela signifie ? Le gradient dans cette région va être faible. Cela donne lieu à un problème de « gradients évanescents ». Hmm. Alors que se passe-t-il lorsque les activations atteignent la partie « quasi-horizontale » de la courbe de part et d’autre ?
Le gradient est petit ou a disparu ( ne peut pas faire de changement significatif à cause de la valeur extrêmement petite ). Le réseau refuse d’apprendre davantage ou est drastiquement lent ( selon le cas d’utilisation et jusqu’à ce que le gradient/calcul soit frappé par des limites de valeurs à virgule flottante ). Il existe des moyens de contourner ce problème et la sigmoïde est encore très populaire dans les problèmes de classification.
Fonction tanh
Une autre fonction d’activation qui est utilisée est la fonction tanh.
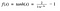
Hm. Cela ressemble beaucoup à la sigmoïde. En fait, c’est une fonction sigmoïde mise à l’échelle!

Ok, maintenant cela a des caractéristiques similaires à la sigmoïde que nous avons discuté ci-dessus. Elle est de nature non linéaire, si bien que nous pouvons empiler des couches ! Elle est liée à l’intervalle (-1, 1), donc pas de souci d’explosion des activations. Un point à mentionner est que le gradient est plus fort pour tanh que pour sigmoïde (les dérivés sont plus raides). Le choix entre sigmoïde et tanh dépendra de vos exigences en matière de force du gradient. Comme la sigmoïde, tanh a également le problème du gradient évanescent.
Tanh est également une fonction d’activation très populaire et largement utilisée.
ReLu
Plus tard, vient la fonction ReLu,
A(x) = max(0,x)
La fonction ReLu est comme indiqué ci-dessus. Elle donne une sortie x si x est positif et 0 sinon.
A première vue, on pourrait croire que cette fonction a les mêmes problèmes qu’une fonction linéaire, car elle est linéaire dans l’axe positif. Tout d’abord, ReLu est non-linéaire par nature. Et les combinaisons de ReLu sont également non linéaires ! ( en fait c’est un bon approximateur. Toute fonction peut être approximée avec des combinaisons de ReLu). Super, donc cela signifie que nous pouvons empiler des couches. Ce n’est pas limité cependant. L’étendue de ReLu est [0, inf). Cela signifie qu’il peut faire exploser l’activation.
Un autre point que je voudrais discuter ici est la sparsité de l’activation. Imaginez un grand réseau neuronal avec beaucoup de neurones. L’utilisation d’une sigmoïde ou d’une tanh fera en sorte que presque tous les neurones se déclenchent de manière analogique ( vous vous souvenez ? ). Cela signifie que presque toutes les activations seront traitées pour décrire la sortie d’un réseau. En d’autres termes, l’activation est dense. Cela est coûteux. Nous voudrions idéalement que quelques neurones du réseau ne s’activent pas et ainsi rendre les activations clairsemées et efficaces.
ReLu nous donne cet avantage. Imaginez un réseau avec des poids initialisés aléatoires ( ou normalisés ) et près de 50% du réseau donne 0 activation en raison de la caractéristique de ReLu ( sortie 0 pour les valeurs négatives de x ). Cela signifie qu’il y a moins de neurones qui tirent (activation clairsemée) et que le réseau est plus léger. Woah, sympa ! ReLu semble être génial ! Oui, il l’est, mais rien n’est impeccable… Pas même ReLu.
À cause de la ligne horizontale dans ReLu( pour X négatif ), le gradient peut aller vers 0. Pour les activations dans cette région de ReLu, le gradient sera 0 à cause duquel les poids ne seront pas ajustés pendant la descente. Cela signifie que les neurones qui se trouvent dans cet état cesseront de répondre aux variations de l’erreur/de l’entrée (simplement parce que le gradient est à 0, rien ne change). C’est ce qu’on appelle le problème du ReLu mourant. Ce problème peut entraîner la mort de plusieurs neurones et les empêcher de réagir, rendant ainsi passive une partie importante du réseau. Il existe des variations dans ReLu pour atténuer ce problème en transformant simplement la ligne horizontale en une composante non horizontale. Par exemple, y = 0,01x pour x<0 en fera une ligne légèrement inclinée plutôt qu’une ligne horizontale. C’est ce qu’on appelle le leaky ReLu. Il existe également d’autres variantes. L’idée principale est de laisser le gradient être non nul et de le récupérer pendant la formation éventuellement.
ReLu est moins coûteux en calcul que tanh et sigmoïde car il implique des opérations mathématiques plus simples. C’est un bon point à prendre en compte lorsque nous concevons des réseaux neuronaux profonds.
Ok, maintenant lequel utilisons-nous ?
Maintenant, quelles fonctions d’activation utiliser. Cela signifie-t-il que nous utilisons juste ReLu pour tout ce que nous faisons ? Ou sigmoïde ou tanh ? Eh bien, oui et non. Lorsque vous savez que la fonction que vous essayez d’approcher a certaines caractéristiques, vous pouvez choisir une fonction d’activation qui approchera la fonction plus rapidement, ce qui accélère le processus d’apprentissage. Par exemple, une sigmoïde fonctionne bien pour un classificateur (voir le graphique de la sigmoïde, ne montre-t-il pas les propriétés d’un classificateur idéal ? ) parce que l’approximation d’une fonction de classificateur en tant que combinaisons de sigmoïde est plus facile que peut-être ReLu, par exemple. Ce qui conduira à un processus de formation et de convergence plus rapide. Vous pouvez également utiliser vos propres fonctions personnalisées. Si vous ne connaissez pas la nature de la fonction que vous essayez d’apprendre, alors je vous suggérerais de commencer avec ReLu, puis de travailler à rebours. ReLu fonctionne la plupart du temps comme un approximateur général !
Dans cet article, j’ai essayé de décrire quelques fonctions d’activation utilisées couramment. Il existe aussi d’autres fonctions d’activation, mais l’idée générale reste la même. La recherche de meilleures fonctions d’activation est toujours en cours. J’espère que vous avez compris l’idée derrière la fonction d’activation, pourquoi elles sont utilisées et comment on décide laquelle utiliser.