L’algorithme de Toom-Cook
On apprend ici une application ingénieuse d’un algorithme diviser pour régner combiné à l’algèbre linéaire pour multiplier de grands nombres, rapidement. Et une introduction à la notation big-O !
En fait, ce résultat est tellement contre-intuitif que le grand mathématicien Kolmogorov a conjecturé qu’un algorithme aussi rapide n’existait pas.
Partie 0 : La multiplication longue est une multiplication lente. (Et une introduction à la notation Big-O)
Nous nous souvenons tous d’avoir appris à multiplier à l’école. En fait, j’ai une confession à faire. Rappelez-vous, c’est une zone sans jugement 😉
À l’école, nous avions des » jeux humides » lorsqu’il pleuvait trop fort pour jouer dans la cour de récréation. Pendant que les autres enfants (normaux/aimant le plaisir/adjectif positif de choix) jouaient à des jeux et s’amusaient, je prenais parfois une feuille de papier et multipliais de grands nombres ensemble, juste pour le plaisir. La joie pure du calcul ! Nous avions même un concours de multiplication, le « Super 144 », où nous devions multiplier une grille de 12 chiffres sur 12 (de 1 à 12) aussi vite que possible. Je m’y suis exercé religieusement, à tel point que j’avais mes propres feuilles d’exercice préparées à l’avance, que je photocopiais et utilisais à tour de rôle. J’ai fini par ramener mon temps à 2 minutes et 1 seconde, moment où ma limite physique de gribouillage était atteinte.
Malgré cette obsession de la multiplication, il ne m’est jamais venu à l’esprit que nous pouvions faire mieux. J’ai passé tant d’heures à multiplier, mais je n’ai jamais essayé d’améliorer l’algorithme.
Considérez la multiplication de 103 par 222.
Nous calculons 2 fois 3 fois 1 +2 fois 0 fois 10 + 2 fois 1 fois 100 + 20 fois 3 fois 1 + 20 fois 0 fois 10 + 20 fois 1 fois 100 = 22800
En général, pour multiplier à des nombres à n chiffres, il faut O(n²) opérations. La notation » big-O » signifie que, si nous devions représenter graphiquement le nombre d’opérations en fonction de n, le terme n² est vraiment ce qui compte. La forme est essentiellement quadratique.
Aujourd’hui, nous allons réaliser tous nos rêves d’enfant et améliorer cet algorithme. Mais d’abord ! Big-O nous attend.
Big-O
Regardez les deux graphes ci-dessous

Demandez à un mathématicien « x² et x²+x^(1/3) sont-ils identiques ? », et il vomira probablement dans sa tasse de café, se mettra à pleurer et marmonnera quelque chose sur la topologie. Du moins, c’était ma réaction (au début), et je ne connais pratiquement rien à la topologie.
Ok. Ce n’est pas la même chose. Mais notre ordinateur ne se soucie pas de la topologie. Les ordinateurs diffèrent en performance de tellement de façons que je ne peux même pas décrire parce que je ne connais rien aux ordinateurs.
Mais il n’y a aucun intérêt à affiner un rouleau compresseur. Si deux fonctions, pour de grandes valeurs de leur entrée, croissent au même ordre de grandeur, alors à des fins pratiques, cela contient la plupart des informations pertinentes.
Dans le graphique ci-dessus, nous voyons que les deux fonctions sont assez similaires pour de grandes entrées. Mais de même, x² et 2x² sont similaires – la seconde est seulement deux fois plus grande que la première. À x = 100, l’une est de 10 000 et l’autre de 20 000. Cela signifie que si nous pouvons calculer l’un, nous pouvons probablement calculer l’autre. Alors qu’une fonction qui croît exponentiellement, disons 10^x, à x = 100 est déjà bien plus grande que le nombre d’atomes dans l’univers. (10¹⁰⁰ >>>> 10⁸⁰ qui est une estimation, le nombre d’Eddington, sur le nombre d’atomes dans l’univers selon mon Googling*).
*en fait, j’ai utilisé DuckDuckGo.
Écrire des entiers comme des polynômes est à la fois très naturel et très peu naturel. Écrire 1342 = 1000 + 300 + 40 + 2 est très naturel. Écrire 1342 = x³+3x²+4x + 2, où x = 10, est légèrement bizarre.
En général, supposons que nous voulons multiplier deux grands nombres, écrits en base b, avec n chiffres chacun. Nous écrivons chaque nombre à n chiffres comme un polynôme. Si nous divisons le nombre à n chiffres en r morceaux, ce polynôme a n/r termes.
Par exemple, laissons b = 10, r = 3, et notre nombre est 142,122,912
Nous pouvons transformer cela en
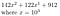
Cela fonctionne très bien lorsque r = 3 et que notre nombre, écrit en base 10, avait 9 chiffres. Si r ne divise pas parfaitement n, nous pouvons simplement ajouter des zéros à l’avant. Encore une fois, cela est mieux illustré par un exemple.
27134 = 27134 + 0*10⁵ = 027134, que nous représentons comme
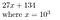
Pourquoi cela peut-il être utile ? Pour trouver les coefficients du polynôme P, si le polynôme est d’ordre N, alors en l’échantillonnant en N+1 points on peut déterminer ses coefficients.
Par exemple, si le polynôme x⁵ + 3x³ +4x-2, qui est d’ordre 5, est échantillonné en 6 points, on peut alors élaborer le polynôme entier.
Intuitivement, un polynôme d’ordre 5 a 6 coefficients : le coefficient de 1, x, x², x³, x⁴, x⁵. Étant donné 6 valeurs et 6 inconnues, nous pouvons trouver les valeurs.
(Si vous connaissez l’algèbre linéaire, vous pouvez traiter les différentes puissances de x comme des vecteurs linéairement indépendants, faire une matrice pour représenter l’information, inverser la matrice, et voilà)
Échantillonnage de polynômes pour déterminer les coefficients (facultatif)
Nous examinons ici un peu plus en profondeur la logique derrière l’échantillonnage d’un polynôme pour déduire ses coefficients. N’hésitez pas à passer à la section suivante.
Ce que nous allons montrer, c’est que si deux polynômes de degré N s’accordent sur N+1 points, alors ils doivent être identiques. C’est-à-dire que N+1 points spécifient de manière unique un polynôme d’ordre N.
Considérons un polynôme d’ordre 2. C’est de la forme P(z) = az² +bz + c. Par le théorème fondamental de l’algèbre – sans vergogne, plug ici, j’ai passé plusieurs mois à mettre en place une preuve de cela, et puis l’écrire, ici – ce polynôme peut être factorisé. Cela signifie que nous pouvons l’écrire comme A(z-r)(z-w)
Notez qu’à z = r, et à z = w, le polynôme s’évalue à 0. Nous disons que w et r sont des racines du polynôme.
Maintenant nous montrons que P(z) ne peut pas avoir plus de deux racines. Supposons qu’il ait trois racines, que nous appelons w, r, s. Nous factorisons alors le polynôme. P(z) = A(z-r)(z-w). Puis P(s) = A(s-r)(s-w). Ce résultat n’est pas égal à 0, car la multiplication de nombres non nuls donne un nombre non nul. Ceci est une contradiction car notre hypothèse initiale était que s était une racine du polynôme P.
Cet argument peut être appliqué à un polynôme d’ordre N d’une manière essentiellement identique.
Maintenant, supposons que deux polynômes P et Q d’ordre N s’accordent sur N+1 points. Alors, s’ils sont différents, P-Q est un polynôme d’ordre N qui est 0 en N+1 points. Par ce qui précède, c’est impossible, car un polynôme d’ordre N a au plus N racines. Ainsi, notre hypothèse a dû être fausse, et si P et Q s’accordent en N+1 points, ils sont le même polynôme.
Voir c’est croire : Un exemple travaillé
Regardons un nombre vraiment énorme que nous appelons p. En base 10, p a 24 chiffres (n=24), et nous allons le diviser en 4 morceaux (r=4). n/r = 24/4 = 6
p = 292,103,243,859,143,157,364,152.
Et que le polynôme qui le représente soit appelé P,
P(x) = 292,103 x³ + 243,859 x² +143,157 x+ 364,152
avec P(10⁶) = p.
Comme le degré de ce polynôme est 3, nous pouvons travailler sur tous les coefficients à partir d’un échantillonnage à 4 endroits. Voyons ce qui se passe quand on l’échantillonne en quelques points.
- P(0) = 364,152
- P(1) = 1,043,271
- P(-1) = 172,751
- P(2) = 3,962,726
Une chose frappante est que ceux-ci ont tous 6 ou 7 chiffres. C’est comparé aux 24 chiffres trouvés à l’origine dans p.
Produisons p par q. Soit q = 124,153,913,241,143,634,899,130, et
Q(x) = 124,153 x³ + 913,241 x²+143,634 x + 899,130
Calculer t=pq pourrait être horrible. Mais au lieu de le faire directement, on essaie de calculer la représentation polynomiale de t, que l’on étiquette T. Comme P est un polynôme d’ordre r-1=3, et Q est un polynôme d’ordre r-1 = 3, T est un polynôme d’ordre 2r-2 = 6.
T(10⁶) = t = pq
T(10⁶) = P(10⁶)Q(10⁶)
L’astuce est que nous allons travailler sur les coefficients de T, plutôt que de multiplier directement p et q ensemble. Ensuite, calculer T(1⁰⁶) est facile, car pour multiplier par 1⁰⁶ on colle juste 6 zéros à l’arrière. Faire la somme de toutes les parties est également facile car l’addition est une action très peu coûteuse pour les ordinateurs.
Pour calculer les coefficients de T, nous devons l’échantillonner à 2r-1 = 7 points, car c’est un polynôme d’ordre 6. Nous voulons probablement choisir de petits entiers, donc nous choisissons
- T(0)=P(0)Q(0)= 364,152*899,130
- T(1)=P(1)Q(1)= 1,043,271*2,080,158
- T(2)=P(2)Q(2)= 3,962,726*5,832,586
- T(-1)=P(-1)Q(-1)= 172751*1544584
- T(-2)=P(-2)Q(-2)= -1,283,550*3,271,602
- T(3)=P(-3)Q(-3)= -5,757,369*5,335,266
Notez la taille de P(-3), Q(-3), P(2), Q(2) etc…. Ce sont tous des nombres ayant approximativement n/r = 24/4 = 6 chiffres. Certains ont 6 chiffres, d’autres 7. Au fur et à mesure que n devient plus grand, cette approximation devient de plus en plus raisonnable.
Jusqu’ici, nous avons réduit le problème aux étapes, ou à l’algorithme, suivants :
(1) Calculer d’abord P(0), Q(0), P(1), Q(1), etc. (action à faible coût)
(2) Pour obtenir nos 2r-1= 7 valeurs de T(x), nous devons maintenant multiplier 2r-1 nombres de taille approximative de n/r chiffres. A savoir, nous devons calculer P(0)Q(0), P(1)Q(1), P(-1)Q(-1), etc. (Action à coût élevé)
(3) Reconstruire T(x) à partir de nos points de données. (Action à faible coût : mais qui entrera en considération plus tard).
(4) Avec notre T(x) reconstruit, évaluer T(10⁶) dans ce cas
Cela conduit joliment à une analyse du temps d’exécution de cette approche.
Temps d’exécution
D’après ce qui précède, nous avons découvert que, en ignorant temporairement les actions à faible coût (1) et (3), le coût de la multiplication de deux nombres à n chiffres avec l’algorithme de Toom obéira à :
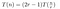
C’est ce que nous avons vu dans l’exemple travaillé. Multiplier chaque P(0)Q(0), P(1)Q(1), etc. coûte T(n/r) car nous multiplions deux nombres de longueur approximative n/r. Nous devons le faire 2r-1 fois, car nous voulons échantillonner T(x) – étant un polynôme d’ordre 2r-2 – à 2r-1 endroits.
Combien est-ce rapide ? On peut résoudre ce genre d’équation de manière explicite.

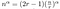
Il ne reste plus qu’à faire un peu de algèbre désordonnée
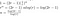
Comme il y avait d’autres coûts du processus de multiplication de la matrice (‘réassemblage’), et de l’addition, nous ne pouvons pas vraiment dire que notre solution est le temps d’exécution exact, donc à la place nous concluons que nous avons trouvé le big-O du temps d’exécution
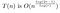
Optimisation de r
Ce temps d’exécution dépend toujours de r. Fixez r, et nous avons terminé. Mais notre curiosité n’est pas encore satisfaite !
A mesure que n devient grand, nous voulons trouver une valeur approximativement optimale pour notre choix de r. C’est-à-dire que nous voulons choisir une valeur de r qui change pour différentes valeurs de n.
La chose clé ici est que, avec r variant, nous devons faire attention au coût de réassemblage – la matrice qui effectue cette opération a un coût de O(r²). Lorsque r est fixe, nous n’avons pas à nous en préoccuper, car lorsque n devient grand avec r fixe, ce sont les termes impliquant n qui déterminent la croissance de la quantité de calcul nécessaire. Comme notre choix optimal de r sera plus grand au fur et à mesure que n devient plus grand, nous ne pouvons plus ignorer cela.
Cette distinction est cruciale. Initialement, notre analyse choisissait une valeur de r, peut-être 3, peut-être 3 milliards, puis regardait la taille du big-O lorsque n devenait arbitrairement grand. Maintenant, nous examinons le comportement lorsque n croît arbitrairement et r croît avec n à un taux que nous déterminons. Ce changement de perspective considère O(r²) comme une variable, alors que lorsque r était maintenu fixe, O(r²) était une constante, bien que nous ne la connaissions pas.
Donc, nous mettons à jour notre analyse d’avant :
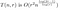
où le O(r²) représente le coût de la matrice de réassemblage. Nous voulons maintenant choisir une valeur de r pour chaque valeur de n, qui minimise approximativement cette expression. Pour minimiser, nous essayons d’abord de différencier par rapport à r. Cela donne l’expression quelque peu odieuse

Normalement, pour trouver le point minimum, nous fixons la dérivée à 0. Mais cette expression n’a pas un joli minimum. Au lieu de cela, nous trouvons une solution » suffisamment bonne « . Nous utilisons r = r^(sqrt(logN)) comme valeur estimée. Graphiquement, cette valeur est assez proche du minimum. (Dans le diagramme ci-dessous, le facteur 1/1000 est là pour rendre le graphique visible à une échelle raisonnable)
Le graphique ci-dessous montre notre fonction pour T(N), mise à l’échelle par une constante, en rouge. La ligne verte est à x = 2^sqrt(logN) qui était notre valeur estimée. ‘x’ prend la place de ‘r’, et dans chacune des trois images, une valeur différente de N est utilisée.



C’est assez convaincant pour moi que notre choix était bon. Avec ce choix de r, nous pouvons le brancher et voir comment le big-O final de notre algorithme:

où nous avons simplement branché notre valeur pour r, et utilisé une approximation pour log(2r-1)/log(r) qui est très précise pour les grandes valeurs de r.
Quel est le degré d’amélioration ?
Peut-être que le fait que je n’ai pas repéré cet algorithme lorsque j’étais un petit garçon faisant des multiplications était raisonnable. Dans le graphique ci-dessous, je donne au coefficient de notre fonction big-O une valeur de 10 (à des fins de démonstration) et je le divise par x² (car l’approche originale de la multiplication était O(n²). Si la ligne rouge tend vers 0, cela montrerait que notre nouveau temps d’exécution fait asymptotiquement mieux que O(n²).
Et en effet, alors que la forme de la fonction montre que notre approche est finalement plus rapide, et finalement elle est beaucoup plus rapide, nous devons attendre jusqu’à ce que nous ayons des nombres longs de près de 400 chiffres pour que ce soit le cas ! Même si le coefficient n’était que de 5, les nombres devraient avoir environ 50 chiffres pour voir une amélioration de la vitesse.

Pour mon moi de 10 ans, multiplier des nombres de 400 chiffres serait un peu exténuant ! Garder la trace des différents appels récursifs de ma fonction serait également quelque peu décourageant. Mais pour un ordinateur effectuant une tâche en IA ou en physique, c’est un problème courant !
Quelle est la profondeur de ce résultat ?
Ce que j’aime dans cette technique, c’est que ce n’est pas de la science infuse. Ce n’est pas la plus époustouflante des mathématiques à découvrir. Rétrospectivement, peut-être que cela semble évident !
Pourtant, c’est la brillance et la beauté des mathématiques. J’ai lu que Kolmogorov a conjecturé dans un séminaire que la multiplication était fondamentalement O(n²). Kolmogorov a essentiellement inventé une grande partie de la théorie moderne des probabilités et de l’analyse. Il était l’un des grands mathématiciens du 20ème siècle. Pourtant, lorsqu’il s’est agi de ce domaine sans rapport, il s’est avéré qu’il y avait tout un corpus de connaissances qui attendait d’être découvert, assis juste sous son nez et celui de tout le monde !
En fait, les algorithmes Diviser et Conquérir viennent assez rapidement à l’esprit aujourd’hui car ils sont si couramment utilisés. Mais ils sont un produit de la révolution informatique, en ce sens que ce n’est qu’avec une vaste puissance de calcul que les esprits humains se sont concentrés spécifiquement sur la vitesse de calcul comme un domaine des mathématiques digne d’être étudié en soi.
C’est pourquoi les mathématiciens ne sont pas seulement prêts à accepter que l’hypothèse de Riemann est vraie juste parce qu’elle semble pouvoir l’être, ou que P n’est pas égal à NP juste parce que cela semble le plus probable. Le monde merveilleux des mathématiques conserve toujours une capacité à confondre nos attentes.
En fait, vous pouvez trouver des moyens encore plus rapides de multiplier. Les meilleures approches actuelles utilisent les transformées de Fourier rapides. Mais je vais garder cela pour un autre jour 🙂
Laissez-moi savoir ce que vous en pensez en bas. Je suis nouvellement sur Twitter comme ethan_the_mathmo, vous pouvez me suivre ici.
Je suis tombé sur ce problème dans un merveilleux livre que j’utilise appelé ‘The Nature of Computation’ par les physiciens Moore et Mertens, où l’un des problèmes vous guide dans l’analyse de l’algorithme de Toom.