Comment aider les élèves qui ont du mal avec les problèmes de mots

« Ils connaissent les mathématiques. Ils ne peuvent simplement pas faire les problèmes de mots. C’est leur compréhension de la lecture. »

Mme Hartwell expliquait pourquoi ses élèves avaient eu des difficultés aux tests d’État. Elle connaissait ses élèves, et avait fait beaucoup d’évaluations. Elle était sûre que leurs difficultés étaient un problème de littératie.

« Je ne comprends pas pourquoi ils rendent la lecture si difficile. Les enfants passent déjà un test de langue. »

J’avais été jumelée avec Mme Hartwell (et d’autres élèves de son école) dans le cadre d’un programme de la ville de New York visant à améliorer les résultats en mathématiques. L’objectif était d’introduire les mathématiques conceptuelles dans les écoles de « niveau 1 ». Les écoles de niveau 1 étaient celles qui étaient en tête de la ville dans trois domaines. Les revenus les plus bas, les résultats aux tests les plus bas et le pourcentage le plus élevé d’élèves de couleur.

J’avais entendu l’explication de la  » littératie  » par d’autres enseignants du programme. Et cela avait du sens. Si les élèves connaissaient les mathématiques, pourquoi sinon avaient-ils des difficultés au test, qui comportait beaucoup de problèmes de mots ?

Mais il y avait un hic. Au cours des trois dernières années, les compétences en littératie étaient passées de 30 % à 40 %, dans toute la ville. Sur la même période, les résultats en mathématiques étaient restés pratiquement inchangés.

Si c’était un problème de lecture, l’augmentation des scores en lecture devrait débloquer une croissance explosive en maths. De plus, le langage dans les problèmes de mots ne semblait tout simplement pas assez compliqué pour causer des problèmes.

La période suivante, j’avais prévu de visiter la classe de Mme Hartwell. Elle avait prévu une leçon sur les problèmes de mots, afin que je puisse voir le problème de première main.

Sur-échafaudage des problèmes de mots

Les élèves étaient assis à des tables rondes, et elle se tenait à l’avant. Elle et ses élèves avaient tous des tableaux blancs portatifs.

Ils ont ouvert leurs manuels à la page 47 et elle a lu un problème de mots à haute voix.  » Sarah a 40 livres de carottes pour ses chevaux. Si elle a 100 chevaux, combien de livres reçoit chaque cheval ? »

« OK classe, elle a 40 livres qu’elle va donner à chaque cheval. Donc quelle opération avons-nous besoin ? »

Elle a montré un tableau d’ancrage listant les  » mots clés  » de chaque opération. ‘Chaque’ était en haut de la liste des divisions.

« Division ! » a répondu la classe.

« Exact. Alors, comment divise-t-on un petit nombre par un grand nombre ? »

La classe est restée silencieuse. Mme Hartwell a dessiné un vinculum (maison de la division longue) sur son tableau blanc. Les élèves ont copié pendant qu’elle mettait 40 sous la maison et 100 à l’extérieur.

« Maintenant, 100 ne rentre pas dans 40, donc nous devons ajouter une décimale. » Elle a changé 40 en 40,0. « Combien de fois 100 va-t-il dans 400 ? »

Quelques étudiants ont crié « Quatre ! »

« Exactement. Maintenant, nous devons également mettre une décimale dans notre quotient. Notre réponse finale est ? »

La classe a lu la réponse, « 0,4 », sur son tableau blanc.

Elle a assigné un problème similaire, et a montré l’affiche « CUBES » sur le mur. « N’oubliez pas d’encercler les chiffres et d’encadrer les mots clés. »

Elle circulait pendant que les élèves travaillaient. Certains demandaient où il fallait mettre la décimale. D’autres avaient du mal à aligner la partie soustraction de la division longue. Certains élèves ont travaillé en binôme, l’un faisant le calcul, tandis que l’autre copiait.

À la fin de la leçon, tout le monde avait la bonne réponse sur sa feuille. « Vous voyez ? » Mme Hartwell a fait remarquer :  » Ils connaissent tous les mathématiques. « 

Qu’est-ce qui n’allait pas ?

Bien qu’il s’agisse d’un exemple extrême, plusieurs des erreurs commises par Mme Hartwell sont en fait assez courantes.

Le sur-affaiblissement se produit lorsque nous fournissons trop de soutien aux élèves. Bien qu’il soit courant que les éducateurs soient fiers de fournir aux élèves  » autant de soutien qu’ils en ont besoin « , le sur-échafaudage est différent.

Le terme  » échafaudage  » provient des travaux de Lev Vygotsky. Il a inventé le terme « zone de développement proximal ». La ZPD comprend les choses qui sont juste hors de portée de l’apprenant. Il ne peut pas tout à fait le faire tout seul, mais il peut le faire avec un soutien. Grâce à  » l’échafaudage « , nous pouvons faire passer ces compétences dans l’ensemble des compétences de base d’un apprenant.

Ce que l’on oublie souvent, c’est que l’échafaudage ne s’applique qu’aux compétences qui se trouvent déjà dans la ZPD d’un apprenant. Il existe toute une série de compétences qui sont actuellement hors de portée de l’apprenant. Lorsque nous essayons d’échafauder ces compétences, nous faisons plus de mal que de bien.

Un des problèmes de l’échafaudage excessif est que les élèves n’intériorisent jamais les compétences ciblées. Lorsque nous aidons un élève avec quelque chose en dehors de sa ZPD, il aura toujours besoin de notre aide. Au moins jusqu’à ce que nous identifions les compétences intermédiaires qui sont dans leur ZPD.

Un autre problème est que le sur-affaiblissement nous donne un faux sentiment de réussite. Dans ce cas, Mme Hartwell croyait que ses élèves pouvaient  » faire le calcul  » dans le problème de mot. En réalité, ils ne faisaient qu’imiter ses actions. Il n’y avait aucune raison de croire qu’ils pouvaient trouver une solution similaire par eux-mêmes.

Elle a également supprimé tout le processus de  » formulation  » du processus de résolution de problèmes. De nombreux éducateurs pensent que la compréhension et la formulation sont la même chose, mais la formulation est une compétence mathématique distincte.

Et c’est peut-être l’ingrédient manquant dans la façon dont vous enseignez actuellement les problèmes de mots.

Ressources pour la classe et apprentissage professionnel

Formulation : La clé du succès des problèmes de mots

Formuler des problèmes de mots implique de les comprendre. Mais cela va plus loin que cela. La formulation s’apparente plus à la traduction qu’à la compréhension.

Lorsqu’un élève lit un problème de mots, il doit d’abord transformer les lettres en sons (décodage). Ensuite, ils doivent comprendre ce que les mots signifient (vocabulaire). Il doit comprendre comment les mots s’assemblent dans une phrase (syntaxe). Enfin, la compréhension vient de l’assemblage de ces éléments pour donner du sens.

La plupart des élèves de 6e année pourraient lire le problème de Mme Hartwell et comprendre facilement que Sarah distribue des carottes à ses chevaux. Mais beaucoup moins feront le lien entre le « partage » des carottes et la division.

C’est la partie qui fait trébucher beaucoup d’éducateurs. Ça nous semble si évident.  » Elle est littéralement en train de diviser les carottes. Comment ne peuvent-ils pas voir que c’est une division ? »

Ils ne le voient tout simplement pas. Si c’était le cas, vous ne verriez pas de tableaux de mots clés accrochés dans les classes de mathématiques. Et tout cela remonte à l’époque où l’on enseigne les opérations pour la première fois.

Pourquoi les élèves se débattent avec la formulation

De nombreux enseignants dans de nombreuses écoles enseignent aux élèves que les mathématiques sont un sujet de fabrication de sens. Mais dans d’autres, les mathématiques sont enseignées comme une matière de mémorisation.

Un exemple de  » maths comme mémorisation  » est lorsque les élèves mémorisent des faits mathématiques. Mais les algorithmes sont aussi des sujets de mémorisation. Mettez 120 au dessus de 47. Suivez ces étapes pour ajouter, celles-ci pour soustraire soustraire, et celles-ci pour multiplier.

Les élèves peuvent répéter ces étapes sans comprendre la taille des nombres ou même la signification des opérations.

Lorsque nous commençons par des concepts (en utilisant des modèles visuels ou des phrases numériques), les élèves apprennent la signification des opérations. Lorsque nous passons directement à un algorithme, les élèves pensent aux opérations comme à une série d’étapes aléatoires.

Année après année, nous demandons aux élèves de se souvenir et de répéter. Ils complètent le même algorithme 30 fois pour les devoirs à la maison. Changez les nombres, et le processus reste le même. Mais donnez-leur un problème de mot, et maintenant ils doivent avoir du sens.

Ce que les tests nous disent sur le raisonnement

Nous pourrions donner à nos élèves 10 problèmes avec le titre « Problèmes de mot de division », pour faciliter les choses. Ils n’auront même pas besoin de lire les problèmes. Ils doivent juste trouver (ou deviner) quel nombre est le diviseur et quel est le dividende.

Mais lorsque les élèves passent un test d’État, l’objectif n’est pas de le rendre plus facile. Le but est d’évaluer ce qu’ils peuvent faire par eux-mêmes.

Les fabricants de tests ne veulent pas leur dire quelle opération utiliser. Ils vont même mettre des mots clés pour la division et l’addition dans le même problème. « Il y a 20 élèves dans la classe. Si chaque enfant a trois dollars, combien ont-ils en tout ? »

Alors, quand les élèves ont du mal avec les problèmes de mots, ce n’est pas seulement à cause des problèmes de mots. Cela signifie généralement qu’ils font des maths de mémoire. Nous devons leur enseigner que les mathématiques consistent à donner du sens.

Les élèves ont besoin de stratégies et de processus pour résoudre les problèmes de mots

Une partie du problème avec un système comme CUBES est qu’il s’appelle lui-même une stratégie, mais c’est en réalité un processus.

Un processus est une série d’étapes. Une fois que vous avez identifié un processus efficace, vous pouvez le répéter encore et encore sans trop y penser. Les algorithmes sont un processus. Tout comme s’aligner du plus grand au plus petit pour aller déjeuner.

Une stratégie est différente. Les stratégies exigent une compréhension profonde. Et la capacité d’appliquer la compréhension dans de nouvelles situations.

Nous ne pouvons pas préparer les élèves à tous les scénarios qu’ils rencontreront dans un problème de mot. Certains exigent qu’ils combinent différentes compétences mathématiques qu’ils n’ont jamais combinées auparavant. Ou ils peuvent exiger que les élèves changent l’ordre des étapes pour arriver à la bonne solution.

Considérez ce qui suit :

Vous avez 5 gallons de jus pour un événement scolaire avec 100 étudiants. Si chaque tasse contient 3 oz, combien de tasses chaque élève peut-il boire ? Combien en restera-t-il.

Un processus de résolution de problèmes peut aider les élèves à commencer à s’attaquer à ce problème. « Identifier ce qui est demandé ». « Considérer quelles informations sont données. »

Mais il n’y a pas de processus fixe que nous pouvons leur enseigner pour réellement le résoudre. C’est là que la stratégie entre en jeu. Ils doivent convertir les unités. Reconnaître que nous divisons avec des restes, plutôt que de diviser complètement. Ils devraient aussi probablement réordonner les opérations, en divisant le jus en tasses avant de diviser par le nombre d’élèves.

Il n’y a pas de « truc » qui va permettre aux élèves d’y arriver. Ils doivent comprendre la signification des opérations. Ils doivent comprendre que les mathématiques sont un sujet de création de sens. Et ils doivent s’exercer de manière répétée à appliquer la pensée stratégique aux problèmes de mots.

Le processus Polya pour résoudre les problèmes de mots

George Pólya était un mathématicien hongrois influent et un professeur de Stanford qui a trouvé un processus pouvant être utilisé pour résoudre n’importe quel problème. Son travail a touché d’innombrables mathématiciens et éducateurs, dont la plupart ne connaissent pas son nom.

En fait, CUBES et d’autres stratégies dites de résolution de problèmes sont vaguement basées sur son travail. Le problème est qu’ils essaient de le simplifier. Dans le processus, ils suppriment tout ce qui ressemble à une réflexion profonde.

Polya croyait que chaque problème pouvait être résolu en quatre étapes : Comprendre, Planifier, Résoudre, et Réfléchir. Je pense que le processus original en quatre étapes de Polya est très bien pour être utilisé dans les écoles.

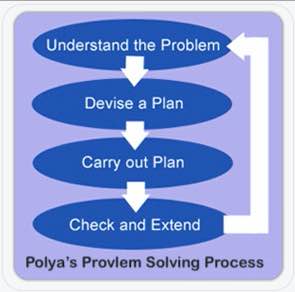Pour comprendre le problème, nous identifions les informations données et ce que nous voulons trouver. C’est de là que vient le  » C  » et le  » U  » des cubes. Si les élèves veulent entourer les chiffres et souligner la question, c’est bien. Je préfère qu’ils les écrivent (avec les unités) dans un organisateur graphique, du moins au début. Cela les aide à traiter ce qu’ils lisent. Cela m’aide également, en tant qu’enseignant, à évaluer leur compréhension lorsque je me promène dans la salle.

Vient ensuite la partie délicate. Le « plan » est l’endroit où nous formulons le problème. Nous prenons un scénario du monde réel et le transformons en une autre représentation mathématique.

La troisième étape est de résoudre. Si nous avons formulé correctement, c’est ici que nous calculons. Les élèves utilisent généralement un algorithme, mais j’encourage l’utilisation d’équations et de modèles visuels également.

Enfin, les élèves regardent en arrière et vérifient leur travail. Ils doivent également réfléchir à leur processus. Si j’ai fait une erreur, pourquoi ? Cette stratégie pourrait-elle m’aider à résoudre des problèmes similaires à l’avenir ?

Stratégies pour résoudre les problèmes de mots

Avoir un processus pour aborder les problèmes de mots est certainement utile. Mais nous ne pouvons pas prétendre que des mathématiques significatives sont apprises simplement en suivant des étapes. Tout l’intérêt des problèmes de mots est d’élargir les mathématiques au-delà des « faits mathématiques » et des algorithmes.

Il existe des stratégies utiles pour aider les élèves à formuler. Au début, j’enseigne explicitement un certain nombre de stratégies différentes.

A mesure que j’enseigne les stratégies, je demande aux élèves de résoudre des problèmes qui vont bien avec cette stratégie. Certains types de problèmes vont très bien avec ‘Devine et vérifie’. D’autres sont plus adaptés à ‘Dessine une image’.

Enfin, je leur donne des problèmes de mots difficiles qui peuvent être résolus de plusieurs façons. Une fois qu’ils ont les outils dans leur ceinture d’outils, ils peuvent choisir celle qui convient le mieux à la situation.

La combinaison de stratégies peut aussi être très efficace. Par exemple, le fait de dessiner une image peut souvent être utile pour aider à la formulation. Si un agriculteur a 18 rangs de carottes et 10 carottes dans chaque rang, un élève peut commencer par dessiner le champ. À un moment donné, il peut penser  » Wow, c’est un tableau  » et réaliser qu’il peut multiplier en utilisant le calcul mental, une expression ou un algorithme.

D’autres fois, les élèves peuvent utiliser des modèles visuels pour formuler et résoudre le problème.

Aidez vos élèves à s’attaquer à des problèmes de mots difficiles

Si vous êtes comme de nombreux enseignants, vous vous inquiétez peut-être de la façon dont vos élèves vont gérer tout cela. Processus, stratégies, pensée critique… il y a beaucoup de choses en jeu.

Vous pouvez même penser que les problèmes de mots semblaient plus faciles avant cet article. Si c’est le cas, je m’en excuse.

La clé est de ne pas se laisser submerger en essayant de tout faire en même temps. Commencez par résoudre un problème de mot simple en utilisant le processus de Polya. Ensuite, introduisez une nouvelle stratégie chaque semaine. À la fin de l’année, vous serez étonné de voir tout le chemin qu’ils ont parcouru.

Vous souhaitez peut-être approfondir la résolution créative de problèmes. Envisagez de participer à un atelier pratique de mathématiques ou de travailler avec un coach en ligne.

Si vous êtes prêt à apporter du Polya dans votre classe demain, cet organisateur graphique est un excellent moyen de commencer. Il étayera le processus en quatre étapes et vous aidera à identifier les endroits où vos élèves font fausse route.

Organisateur gratuit de problèmes de mots

À propos de l’auteur

Jeff Lisciandrello est le fondateur de Room to Discover et un consultant en éducation spécialisé dans l’apprentissage centré sur l’élève. Sa conception de l’apprentissage en 3 ponts aide les écoles à explorer des pratiques innovantes dans des cadres traditionnels. Il aime aider les éducateurs à adopter des approches de l’enseignement fondées sur l’enquête et personnalisées. Vous pouvez le contacter via Twitter @EdTechJeff

.