Introduction
Cette page passe en revue l’équation de continuité, qui impose la conservation de la masse dans une analyse eulérienne. Ce n’est pas strictement une description du comportement matériel, mais l’équation résultante est souvent utilisée comme une identité pour manipuler algébriquement les modèles constitutifs décrivant le comportement matériel. Elle mérite donc d’être examinée. Elle est également centrale pour l’analyse de l’écoulement des fluidesparce que les analyses classiques des fluides ne peuvent pas être lagrangiennes puisque les positions de toutes les particules de fluide à \(t = 0\) sont inconnues.
Conservation de la masse
L’équation de continuité reflète le fait que la masse est conservée dans toute analyse de mécanique continue non nucléaire. L’équation est développée en additionnant le taux auquel la masse entre et sort d’un volume de contrôle, et en fixant le flux net entrant égal au taux de changement de masse à l’intérieur de celui-ci. Ceci est démontré dans la figure ci-dessous.
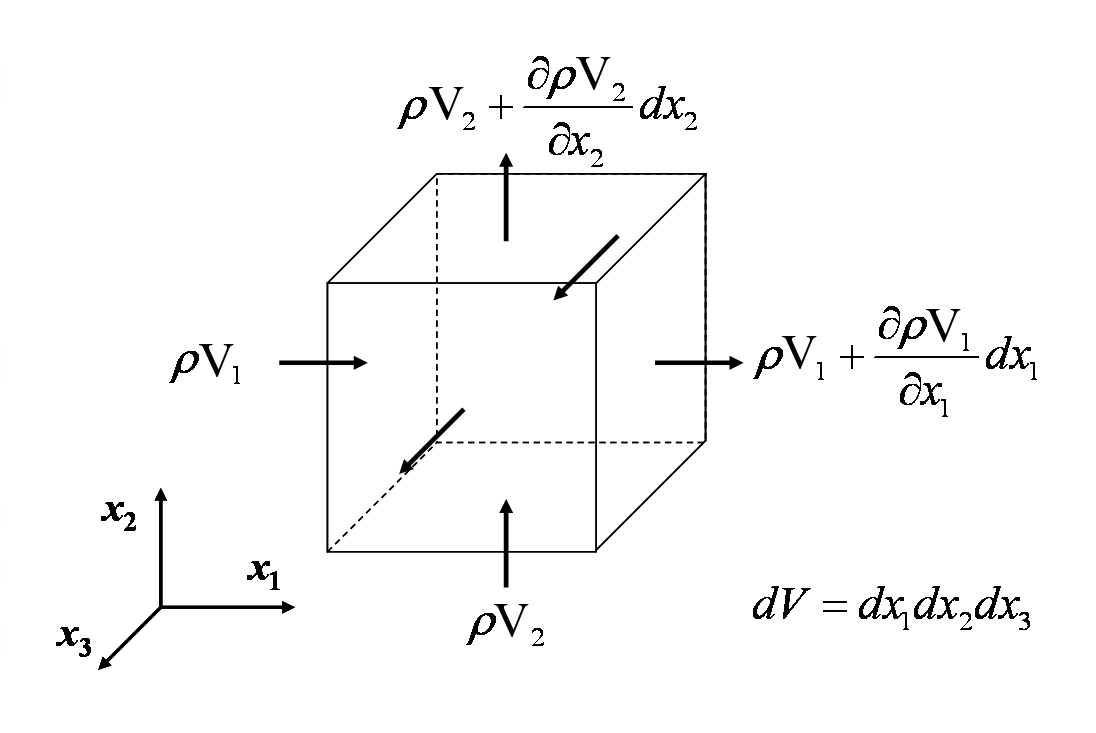
L’équation de tous les débits massiques entrant et sortant du volume de contrôle différentiel donne
L’annulation des termes et la division par \(dx_1 dx_2 dx_3\) donne
et en réarrangeant on obtient
\
Ceci peut être écrit de façon concise comme
\

Points importants
Ce sont les formes finales, complète et la plus générale des formes de l’équation de continuité qui applique la conservation de la masse. Elle s’applique à tous les matériaux, pas seulement aux fluides. Elle s’applique donc aussi aux solides. Notez que c’est une équation scalaire unique et qu’elle est de nature eulérienne parce que les termes de gradient sont \({\partiel \over \partiel x_i}\), et non \({\partiel \over \partiel X_i}\).
On pourrait se demander s’il existe une contrepartie lagrangienne à la forme eulérienne de ceci. C’est le cas. Elle s’écrit généralement comme suit
\
Ceci indique simplement que le morceau différentiel de masse dans l’état déformé\(\rho \, dV\) doit être égal à sa valeur originale\(\rho_o dV_o\) dans l’état non déformé.
Il existe plusieurs cas particuliers de l’équation de continuité. Le premier se produit lorsque l’écoulement est en régime permanent. Dans ce cas, la dérivée par rapport au temps est nulle, ce qui laisse.
\
Le deuxième cas particulier est celui de l’incompressibilité, c’est-à-dire, \(\rho = \)constant.Dans ce cas, la dérivée par rapport au temps est nulle et \(\rho\) peut être éliminé de l’équation laissant seulement
\
Ce résultat est assez simple pour qu’il soit souvent développé.
Notez que ce n’est rien de plus que \(\text{tr}({\bf D}) = 0\) pour le cas des matériaux incompressibles.

Dérivée du matériau
Ce qui suit mérite d’être souligné car il permet de séparer la densité et le vecteur vitesse. La première étape consiste à appliquer la règle du produit au terme de divergence de l’équation de continuité.
\
Et ensuite, on remarque que\({\partial \rho \over \partial t} + {\bf v} \cdot \nabla \rho\)est juste la dérivée matérielle de la densité,\({D \rho \over D t}\).
Donc l’équation de continuité peut aussi être écrite comme
\
Si le matériau est incompressible, alors \(\rho\) ne peut pas changer, donc \( {D \rho \over D t} \) doit être zéro, laissant
\
Et ensuite diviser par \(\rho\) (puisqu’il n’est pas zéro) pour obtenir
\

Equation de continuité Exemple
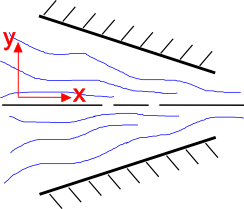
Il est intuitif que l’écoulement d’un fluide s’accélère lorsque l’aire de la section transversale diminue, comme indiqué à droite. L’équation de continuité explique ce phénomène. Considérons un champ d’écoulement bidimensionnel en régime permanent d’un fluide incompressible. L’équation de continuité pour cette situation est la suivante :
\
Commencez par examiner la composante y de l’écoulement, \(v_2\). La géométrie de la buse convergente force la composante \(v_2\) à s’écouler vers le haut lorsque \(y \lt 0\) et à s’écouler vers le bas lorsque \(y \gt 0\). Donc \(v_2 \gt 0\) quand\(y \lt 0\) et \(v_2 \lt 0\) quand \(y \gt 0\).
L’effet net de ceci est que \({\partiel v_2 \over \partiel x_2} \lt 0\)dans la tuyère convergente.
Mais l’équation de continuité impose que la somme des deux dérivées partielles soit égale à zéro. Donc, si la seconde est inférieure à zéro, alors
\
Et cela signifie que l’écoulement du fluide doit être accéléré.